parāvartya yojayet-Divide: (2×3+3×2−4x+15)(x+3)

by
Vedic Math Analysis

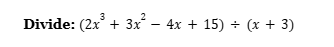
Vedic Math Analysis

Core Principle / Theory

परावर्त्य योजयेत् (Paravartya Yojayet) वैदिक गणित का एक शक्तिशाली सूत्र है, जिसका अर्थ है ‘पक्षांतरण करें और लागू करें’ (Transpose and Apply)। बीजगणित में, जब हम किसी बहुपद को (x + a) या (x – a) जैसे भाजक से विभाजित करते हैं, तो हम स्थिरांक का चिन्ह बदल देते हैं (जैसे +3 को -3 में) और फिर लंबी विभाजन प्रक्रिया के बजाय केवल गुणा और जोड़ का उपयोग करते हैं। यह विधि सिंथेटिक डिवीजन (Synthetic Division) के समान है लेकिन अधिक व्यापक है।

परावर्त्य विधि द्वारा हल

Steps:

  • चरण 1: भाज्य (Dividend) के गुणांक लिखिए: 2, 3, -4, 15।
  • चरण 2: भाजक (Divisor) ‘x + 3’ है। परावर्त्य नियम के अनुसार, +3 का चिन्ह बदलकर -3 लें।
  • चरण 3: पहले गुणांक ‘2’ को वैसे ही नीचे उतारें।
  • चरण 4: अब 2 को -3 से गुणा करें (-6) और इसे अगले गुणांक 3 में जोड़ें। (3 – 6 = -3)।
  • चरण 5: प्राप्त -3 को -3 से गुणा करें (9) और इसे अगले गुणांक -4 में जोड़ें। (-4 + 9 = 5)।
  • चरण 6: अंत में, 5 को -3 से गुणा करें (-15) और इसे अंतिम गुणांक 15 में जोड़ें। (15 – 15 = 0)।
  • चरण 7: अंतिम मान 0 शेषफल (Remainder) है। बचे हुए अंक (2, -3, 5) भागफल के गुणांक हैं। अतः उत्तर: 2x² – 3x + 5।

Visual Representation:

text
Divisor | Dividend Coefficients
 (x+3)  |   2      3     -4     15
--> -3  |         -6      9    -15
--------|--------------------------
        |   2     -3      5      0

Quotient Coefficients: 2, -3, 5
Remainder: 0

Final Answer: 2x^2 - 3x + 5

पारंपरिक लंबी विभाजन विधि

Steps:

  • चरण 1: 2x³ को x से विभाजित करें, परिणाम 2x² आता है। इसे ऊपर लिखें।
  • चरण 2: 2x² को पूरे भाजक (x + 3) से गुणा करें = 2x³ + 6x²। इसे भाज्य के नीचे लिखकर घटाएं। शेष: -3x²।
  • चरण 3: अगला पद -4x नीचे लाएं। अब -3x² को x से विभाजित करें, परिणाम -3x आता है।
  • चरण 4: -3x को (x + 3) से गुणा करें = -3x² – 9x। इसे घटाएं (चिन्ह बदलें)। शेष: 5x।
  • चरण 5: अंतिम पद 15 नीचे लाएं। 5x को x से विभाजित करें, परिणाम +5 आता है।
  • चरण 6: 5 को (x + 3) से गुणा करें = 5x + 15। घटाने पर शेषफल 0 प्राप्त होता है।

आधुनिक अनुप्रयोग

  • डिजिटल सिग्नल प्रोसेसिंग (DSP): फिल्टर डिजाइन और सिग्नल विश्लेषण में बहुपद गणनाओं के लिए।
  • क्रिप्टोग्राफी: Reed-Solomon जैसे त्रुटि सुधार कोड (Error Correction Codes) में इसका उपयोग होता है।
  • कंप्यूटर बीजगणित: सिम्बॉलिक कंप्यूटेशन सॉफ्टवेयर में बहुपद विभाजन को तेज़ बनाने के लिए।
  • CRC (Cyclic Redundancy Check): डेटा ट्रांसमिशन में त्रुटियों का पता लगाने के लिए बाइनरी बहुपद विभाजन में।