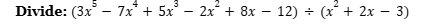
Vedic Math Analysis

Core Principle / Theory

वैदिक गणित का ‘परावर्त्य योजयेत्’ (Paravartya Yojayet) सूत्र बीजगणितीय विभाजन के लिए अत्यंत शक्तिशाली है। इसका शाब्दिक अर्थ है ‘पक्षांतरण करें और लागू करें’ (Transpose and Apply)। इस विधि में, हम भाजक (Divisor) के पदों के चिह्नों को बदल देते हैं (परावर्त्य) और फिर भाग की जटिल प्रक्रिया को सरल गुणा और जोड़ (योजयेत्) में बदल देते हैं। यह विधि लंबी विभाजन प्रक्रिया (Long Division) की तुलना में बहुत तेज और त्रुटि-मुक्त है।

परावर्त्य योजयेत् विधि द्वारा हल

Steps:

चरण 1: भाजक (Divisor) $x^2 + 2x – 3$ है। पहले पद $x^2$ को छोड़ दें और शेष पदों $+2x$ और $-3$ के चिह्न बदलें। हमारे ‘परावर्त्य’ गुणक (multipliers) होंगे: $-2$ और $+3$।
चरण 2: भाज्य (Dividend) के गुणांकों को एक पंक्ति में लिखें: $3, -7, 5, -2, 8, -12$।
चरण 3: पहले गुणांक $3$ को सीधे नीचे उत्तर की पंक्ति में उतारें।
चरण 4: इस $3$ को गुणकों $(-2, 3)$ से गुणा करें। परिणाम $-6$ और $9$ को अगले दो गुणांकों के नीचे लिखें।
चरण 5: दूसरे स्तंभ को जोड़ें: $-7 + (-6) = -13$। यह भागफल का दूसरा पद है।
चरण 6: अब $-13$ को गुणकों $(-2, 3)$ से गुणा करें $\rightarrow 26$ और $-39$। इन्हें अगले स्तंभों में एक स्थान आगे खिसका कर लिखें।
चरण 7: तीसरे स्तंभ को जोड़ें: $5 + 9 + 26 = 40$।
चरण 8: अब $40$ को $(-2, 3)$ से गुणा करें $\rightarrow -80$ और $120$। इन्हें आगे लिखें।
चरण 9: चौथे स्तंभ को जोड़ें: $-2 – 39 – 80 = -121$।
चरण 10: अंत में $-121$ को $(-2, 3)$ से गुणा करें $\rightarrow 242$ और $-363$।
चरण 11: अंतिम दो स्तंभों (शेषफल भाग) को जोड़ें। $x$ का गुणांक: $8 + 120 + 242 = 370$ और अचर पद: $-12 – 363 = -375$।
परिणाम: भागफल (Quotient) = $3x^3 – 13x^2 + 40x – 121$ और शेषफल (Remainder) = $370x – 375$।

Visual Representation:

text
Divisor: x^2 + 2x - 3
Modified Multipliers: -2, +3

   -2, +3 |   3    -7     5     -2      8     -12
          |        -6     9
          |              26    -39
          |                    -80    120
          |                           242    -363
----------------------------------------------------
          |   3   -13    40    -121  |  370    -375

Quotient  : 3x^3 - 13x^2 + 40x - 121
Remainder : 370x - 375

पारंपरिक लंबी विभाजन विधि (Long Division)

Steps:

चरण 1: $3x^5$ को $x^2$ से भाग दें $\rightarrow 3x^3$। पूरे भाजक को $3x^3$ से गुणा करें और घटाएं।
चरण 2: घटाने पर प्राप्त नए बहुपद का पहला पद $-13x^4$ होगा। इसे $x^2$ से भाग दें $\rightarrow -13x^2$।
चरण 3: $-13x^2$ से भाजक को गुणा करें और फिर से घटाएं।
चरण 4: यह प्रक्रिया तब तक दोहराएं जब तक कि शेषफल की घात भाजक की घात से कम न हो जाए।
कठिनाई: इस विधि में बार-बार गुणा करना, चिह्न बदलना और घटाना पड़ता है, जिससे समय अधिक लगता है और गलती होने की संभावना अधिक होती है।

आधुनिक अनुप्रयोग (Modern Applications)

डिजिटल सिग्नल प्रोसेसिंग (DSP): फिल्टर डिजाइन और सिग्नल विश्लेषण में बहुपद विभाजन का उपयोग होता है।
क्रिप्टोग्राफी (Cryptography): डेटा एन्क्रिप्शन और त्रुटि सुधार कोड (जैसे Reed-Solomon codes) में गैलोइस फील्ड (Galois Field) पर बहुपद विभाजन का भारी उपयोग होता है।
कंप्यूटर अलजेब्रा सिस्टम (CAS): सिम्बोलिक गणना सॉफ़्टवेयर (जैसे Mathematica, MATLAB) में तेज गणना के लिए।
CRC जनरेशन: डेटा ट्रांसमिशन में त्रुटियों का पता लगाने के लिए साइक्लिक रिडंडेंसी चेक (CRC) बहुपद विभाजन पर ही आधारित है।