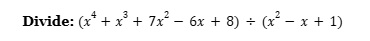
Vedic Math Analysis

Core Principle / Theory

‘परावर्त्य योजयेत्’ (Paravartya Yojayet) वैदिक गणित का एक शक्तिशाली सूत्र है, जिसका अर्थ है ‘पक्षांतरण करें और लागू करें’ (Transpose and Apply)। बहुपद विभाजन (Polynomial Division) में, यह विधि भाजक (Divisor) के गुणांकों के चिह्न बदलकर (Sign Change) विभाजन को सरल जोड़ और गुणा की प्रक्रिया में बदल देती है। यह विधि विशेष रूप से तब उपयोगी होती है जब भाजक x-1 या x+1 के रूप में न होकर द्विघात (Quadratic) या उच्चतर घात का हो।

वैदिक विधि: परावर्त्य योजयेत्

Steps:

• चरण 1: भाजक (Divisor) x² – x + 1 है। x² को छोड़कर, शेष गुणांक -1 और +1 हैं। इनके चिह्न बदलें: ये +1 और -1 हो जाएंगे (ये हमारे ‘संशोधित गुणक’ हैं)।
• चरण 2: भाज्य (Dividend) के गुणांक लिखें: 1, 1, 7, -6, 8। चूँकि भाजक की घात 2 है, इसलिए अंतिम 2 अंकों को शेषफल (Remainder) के लिए अलग करें।
• चरण 3: पहला गुणांक ‘1’ सीधे नीचे उतारें।
• चरण 4: इस ‘1’ को संशोधित गुणकों (1, -1) से गुणा करें और अगले दो गुणांकों के नीचे लिखें। दूसरा कॉलम जोड़ें: 1 + 1 = 2।
• चरण 5: अब परिणाम ‘2’ को संशोधित गुणकों (1, -1) से गुणा करें और अगले कॉलमों में जोड़ें। तीसरा कॉलम जोड़ें: 7 – 1 + 2 = 8।
• चरण 6: अब परिणाम ‘8’ को संशोधित गुणकों (1, -1) से गुणा करें और शेषफल वाले भाग में जोड़ें।
• चरण 7: शेषफल कॉलम जोड़ें: (-6 – 2 + 8 = 0) और (8 – 8 = 0)।
• परिणाम: भागफल गुणांक (1, 2, 8) -> x² + 2x + 8 और शेषफल 0 है।

Visual Representation:

text
Divisor: x^2 - x + 1
Modified Multipliers: +1, -1

      |  1   1   7  : -6   8   (Dividend Coeffs)
 +1   |      1  -1  :          (1 * 1, -1)
 -1   |          2  : -2       (2 * 1, -1)
      |             :  8  -8   (8 * 1, -1)
----------------------------------
      |  1   2   8  :  0   0
      |  x^2 x   c  :  R   R

Quotient  = x^2 + 2x + 8
Remainder = 0

पारंपरिक लंबी विभाजन विधि (Long Division)

Steps:

• चरण 1: x⁴ को x² से विभाजित करें, भागफल x² प्राप्त होता है। भाजक को x² से गुणा करें और भाज्य से घटाएं।
• चरण 2: शेष बहुपद 2x³ + 6x² – 6x + 8 प्राप्त होता है। अब 2x³ को x² से विभाजित करें, भागफल +2x प्राप्त होता है।
• चरण 3: भाजक को 2x से गुणा करें और घटाएं। शेष 8x² – 8x + 8 प्राप्त होता है।
• चरण 4: अंत में, 8x² को x² से विभाजित करें, भागफल +8 प्राप्त होता है। गुणा करें और घटाएं।
• चरण 5: अंतिम शेषफल 0 प्राप्त होता है। यह प्रक्रिया लंबी है और इसमें बीजगणितीय घटाव में गलती होने की संभावना अधिक रहती है।

आधुनिक अनुप्रयोग (Modern Applications)

• डिजिटल सिग्नल प्रोसेसिंग (DSP): IIR और FIR फिल्टर डिजाइन में बहुपद विभाजन का उपयोग होता है, जहाँ वैदिक विधि गणना को तेज़ कर सकती है।
• कोडिंग थ्योरी (Coding Theory): CRC (Cyclic Redundancy Check) और एरर करेक्शन कोड्स (Reed-Solomon codes) में बड़े बहुपदों का विभाजन आवश्यक होता है।
• क्रिप्टोग्राफी (Cryptography): एलिप्टिक कर्व क्रिप्टोग्राफी और अन्य पब्लिक-की सिस्टम में मॉडुलर अंकगणित और बहुपद संचालन में उपयोगी।
• कंप्यूटर अलजेब्रा सिस्टम (CAS): प्रतीकात्मक गणना (Symbolic Computation) सॉफ़्टवेयर में एल्गोरिदम को अनुकूलित करने के लिए।