Sanskrit Shlok Analysis

Original Verse

गुण्यान्त्यमङ्को गुणकेन हन्यादुत्सारितेनैवोपान्त्यमादीन्।

गुण्यस्त्वधोऽधो गुणिखण्डतुल्यस्तैः खण्डकैः संगुणितो युतो वा।

भवो गुणैः शुध्यति येन तेन लब्ध्या च गुण्यो गुणितैः फलं वा।

द्विधा भवेत् रूपविभाग एवम् स्थानैः पृथग्वा गुणितैः समस्तैः।

इष्टोन्युग्मेन गुणेन दनघ्नोऽभीष्टघ्नगुण्यान्वित वञ्जितो वा॥

Hindi Translation

गुणक से गुण्य के अंतिम अंक को गुणा करें, और फिर (परिणाम को) आगे हटाकर (स्थान बदलकर) उपान्त्य (दूसरे अंतिम) और आदि (प्रारंभिक) अंकों को भी इसी प्रकार गुणा करें। गुणित किया जाने वाला गुण्य (multiplicand) तो नीचे-नीचे (एक के बाद एक पंक्तियों में) गुणक के खंडों (भागों) के समान (स्थापित किया जाए)। उन खंडों द्वारा या तो गुणा किया जाए या (अंत में) जोड़ा जाए। वह परिणाम उन गुणों (गुणा करने वाले कारकों/विधियों) से शुद्ध (सही) होता है, और प्राप्त लब्धि (भागफल) तथा गुणा किए गए गुण्यों द्वारा भी परिणाम प्राप्त होता है। इस प्रकार अंकों का विन्यास (रूप-विभाग) दो प्रकार से हो सकता है: या तो स्थानमानों (place values) के अनुसार अलग-अलग गुणा करके, या समस्त (पूरे) संख्या को एक साथ गुणा करके। एक गुणक, जो किसी 'अभीष्ट' (इच्छित) संख्या से कम किए गए 'युग्म' (गोल संख्या या दस, सौ आदि) के रूप में हो, से गुणा करते समय, गुण्य को पहले उस 'युग्म' संख्या ('दन') से गुणा करें, और फिर 'अभीष्ट' संख्या से गुणा किए गए गुण्य को उसमें से घटाएं या जोड़ें।

Word-by-Word Analysis

Word	Root (Dhatu/Shabda)	Hindi Meaning	English Equivalent	English Con
गुण्यान्त्यमङ्को	गुण्यान्त (गुण्य+अन्त) + अङ्क (Shabda)	गुण्‍य (जिसको गुणा करना है) का अंतिम अंक	last digit of the multiplicand	The digit at the units place of the number being multiplied.
गुणकेन	गुणक (Shabda), तृतीया एकवचन	गुणक (जिससे गुणा करना है) के द्वारा	by the multiplier	Using the number that multiplies another.
हन्यात्	हन् (Han Dhatu – to strike, to multiply), विधिलिङ् प्रथमपुरुष एकवचन	गुणा करे	should multiply	The action of performing multiplication.
उत्सारितेनैव	उत्सारित (उद् + सृ Dhatu + क्त प्रत्यय) + एव (Avyaya)	आगे हटाकर ही (स्थान परिवर्तित करके)	by moving forward/shifting	By displacing the number to a higher place value, effectively shifting its position.
उपान्त्यमादीन्	उपान्त्य (Shabda) + आदि (Shabda), द्वितीया बहुवचन	उपान्त्य (अंतिम से पहले) और आदि (प्रारंभिक) अंकों को	second-to-last and so on to the first digits	Referring to the digits from the second-to-last position all the way to the first (leftmost) digit.
गुण्यस्त्वधोऽधो	गुण्य (Shabda) + तु (Avyaya) + अधस् (Avyaya) (repeated)	गुण्‍य (जिसको गुणा करना है) तो नीचे-नीचे	the multiplicand, successively below	The number being multiplied, placed one below the other in successive steps of calculation.
गुणिखण्डतुल्यस्तैः	गुणिखण्डतुल्य (गुणक+खण्ड+तुल्य) (Shabda) + तैः (तद् Shabda, तृतीया बहुवचन)	गुणक के खंडों के समान उन (खंडों) से	equal to the parts/segments of the multiplier, by them	Referring to the individual parts or digits into which the multiplier is broken down, and using those parts.
खण्डकैः	खण्डक (Shabda), तृतीया बहुवचन	खंडों के द्वारा (भागों द्वारा)	by the segments/parts	Using the individual divisions or components of a number.
संगुणितो	सम् + गुणि (Saṃ + Guṇ Dhatu – to multiply) + क्त प्रत्यय	गुणा किया गया	multiplied	The state of having been multiplied.
युतो	यु (Yu Dhatu – to join, to add) + क्त प्रत्यय	जोड़ा गया	added	The state of having been added.
भवो	भू (Bhū Dhatu – to be, to become, here product/result)	परिणाम/फल	the product/result	The outcome or total obtained after calculation.
गुणैः	गुण (Shabda), तृतीया बहुवचन	गुणों/अंकों द्वारा (या गुणन क्रिया द्वारा)	by factors/digits/multiplications	Through the use of digits, factors, or by the process of multiplication itself.
शुध्यति	शुध् (Śudh Dhatu – to purify, to be correct), लट् प्रथमपुरुष एकवचन	शुद्ध होता है/सही गणना होती है	becomes correct/is calculated	The result is validated or accurately obtained.
लब्ध्या	लभ् (Labh Dhatu – to obtain) + क्तिन् प्रत्यय, तृतीया एकवचन	लब्धि (भागफल) द्वारा	by the quotient/obtained result	Using the result obtained from division or any intermediate calculation.
गुणितैः	गुणि (Guṇ Dhatu – to multiply) + क्त प्रत्यय, तृतीया बहुवचन	गुणित किए गए (अंकों/संख्याओं) के द्वारा	by the multiplied (numbers/factors)	Using the numbers that have been multiplied.
फलं	फल (Shabda)	फल/परिणाम	product/result	The final outcome of the calculation.
द्विधा	द्वि (Dvi Shabda) + धा (suffix for 'in two ways')	दो प्रकार से	in two ways	Indicating two different methods or classifications.
रूपविभाग	रूप (Shabda) + विभाग (Shabda)	स्वरूप का विभाजन/अंकों का विन्यास	division of forms/arrangement of numbers	How the numbers or their forms are categorized or organized.
स्थानैः	स्थान (Sthāna Shabda – place, position), तृतीया बहुवचन	स्थानों (स्थानमानों) द्वारा	by place values/positions	Referring to the positional value of digits (units, tens, hundreds, etc.).
पृथग्वा	पृथक् (Avyaya) + वा (Avyaya)	या अलग-अलग	or separately	As distinct, individual components.
समस्तैः	समस्त (Samasta Shabda – all, collective), तृतीया बहुवचन	समस्त (समूचे) के द्वारा	by all/collectively	Considering all parts together as a whole.
इष्टोन्युग्मेन	इष्ट (desired) + ऊन (less) + युग्म (pair/even/round number) (Shabda), तृतीया एकवचन	अभीष्ट (इच्छित) से कम किए गए युग्म (गोल संख्या जैसे दस, सौ) से	by the multiplier (or number) which is (a desired quantity) less than a round/even number	A technique where a multiplier (e.g., 9) is considered as a round number (10) minus a desired quantity (1). 'युग्म' refers to the round number, 'इष्टोन' refers to the desired quantity subtracted from it.
गुणेन	गुण (Shabda), तृतीया एकवचन	गुणक से/गुणा करने से	by the multiplier/by multiplication	The agent or means of multiplication.
दनघ्नोऽभीष्टघ्नगुण्यान्वित	दन (implicit reference to the 'round number' from इष्टोनयुग्मेन, e.g., दश) + घ्न (Dhatu, to multiply) + अभीष्टघ्न (अभीष्ट + घ्न) + गुण्य + अन्वित (past participle)	दन (उस गोल संख्या) से गुणा किया हुआ, और अभीष्ट (इच्छित संख्या) से गुणा किए हुए गुण्य से युक्त	multiplied by 'dan' (the implied round number, e.g., ten), accompanied by the multiplicand multiplied by the desired number	Describes a step where the multiplicand is first multiplied by the 'round number' (e.g., 10 for 9) and then combined with the multiplicand multiplied by the 'desired quantity' (e.g., 1 for 9).
वञ्जितो	वञ्च् (Vañch Dhatu – to cheat, to subtract, to trick) + क्त प्रत्यय	घटाया गया/वंचित किया गया	subtracted/deprived	In mathematical cons, it often implies subtraction or a manipulation that reduces the quantity.

---

---

1. रूप गुणा (3.2.1)
   

---

सूत्र की मुख्य पंक्ति:

“द्विधा भवेत् रूपविभाग एवम् स्थानैः पृथग्वा गुणितैः समस्तैः।”

शब्दार्थ:

• द्विधा = दो प्रकार से / दो हिस्सों में
  
• भवेत् = हो सकता है / होता है
  
• रूपविभाग = रूपों में विभाजन
  
• एवम् = इस प्रकार
  
• स्थानैः = स्थानों के अनुसार (दहाई, सैकड़ा आदि)
  
• पृथक् वा = अलग‑अलग भी
  
• गुणितैः = गुणा करके
  
• समस्तैः = सबके एक साथ (जोड़कर)
  

सरल अर्थ (रूप गुणा से संबंध):

इस पंक्ति में कहा है कि:

• संख्या का विभाजन रूपों में किया जा सकता है,
  
• जैसे गुणक को आसान रूप में बाँटना –
  

• 12 = 10 + 2
  
• 15 = 10 + 5
  

• फिर उन रूपों से अलग‑अलग गुणा करके,
  
• सब परिणामों को जोड़कर अंतिम उत्तर पाया जाता है।
  

यही “रूप विभाजन” → “रूप गुणा” की विधि है।

उदाहरण ढांचा:

236 × 12

• 12 = 10 + 2
  
• 236 × 12 = 236 × 10 + 236 × 2
  

---

2. स्थान गुणा (3.2.2)
   

---

इसी पंक्ति का दूसरा पक्ष:

“द्विधा भवेत् रूपविभाग एवम् स्थानैः पृथग्वा गुणितैः समस्तैः।”

यहाँ “स्थानैः” शब्द से “स्थान गुणा” निकलता है।

शब्दार्थ (जो हमारे काम का है):

• स्थानैः = स्थानों (एकाई, दहाई, सैकड़ा) के आधार पर
  
• पृथक् = अलग‑अलग
  
• गुणितैः = गुणा करके
  
• समस्तैः = सबको जोड़कर
  

सरल अर्थ (स्थान गुणा से संबंध):

• संख्या को उसके स्थान मूल्यों के आधार पर तोड़ते हैं:
  

• 14 = 10 + 4
  
• 205 = 200 + 5
  

• हर स्थान वाले भाग से अलग‑अलग गुणा करते हैं,
  
• फिर सबको जोड़कर उत्तर लेते हैं।
  

यही है “स्थान गुणा” की विधि।

उदाहरण ढांचा:

23 × 14

• 14 = 10 + 4
  
• 23 × 14 = 23 × 10 + 23 × 4
  

---

3. विभाग गुणा (3.2.3)
   

---

“रूपविभाग” वाला शब्द यहाँ मुख्य है:

“द्विधा भवेत् रूपविभाग एवम्…”

द्विधा भवेत् रूपविभाग एवम्।

स्थानैः पृथग्वा गुणितैः समस्तैः॥

• द्विधा भवेत् = दो तरह से हो सकता है
• रूपविभाग = रूपों में विभाजन
• स्थानैः पृथक् = स्थानों के अनुसार अलग‑अलग
• गुणितैः समस्तैः = गुणा करके सबको जोड़कर

शब्दार्थ:

• विभाग = विभाजन, भागों में बाँटना
  
• रूपविभाग = रूपों या हिस्सों में विभाजन
  

सरल अर्थ (विभाग गुणा से संबंध):

• बड़ी संख्या को सुविधाजनक भागों में बाँट देते हैं:
  

• 47 = 40 + 7
  
• 123 = 100 + 20 + 3
  

• फिर हर भाग का गुणा करते हैं,
  
• और सबको जोड़ देते हैं।
  

अंतर यह है कि:

• रूप गुणा में हम अक्सर गुणक को रूपों में बाँटते हैं,
  
• विभाग गुणा में मुख्य ज़ोर गुण्य को भागों में बाँटने पर होता है।
  

उदाहरण ढांचा:

47 × 6

• 47 = 40 + 7
  
• 47 × 6 = 40 × 6 + 7 × 6
  

---

4. खण्ड गुणा (3.2.4)
   

---

सूत्र की पंक्ति (खण्ड से संबंधित):

“गुण्यस्त्वधोऽधो गुणिखण्डतुल्यस्तैः खण्डकैः संगुणितो युतो वा।”

शब्दार्थ:

• गुण्यः = जिसे गुणा करते हैं
  
• तु = तो
  
• अधः अधः = नीचे‑नीचे (क्रम से)
  
• गुणिखण्डतुल्यस्तैः = गुणक के खण्डों के समान रहने वाले
  
• खण्डकैः = खण्डों से / टुकड़ों से
  
• संगुणितः = गुणा किया हुआ
  
• युतः = जोड़ा हुआ
  
• वा = या
  

सरल अर्थ:

• गुण्य (ऊपर की संख्या) को नीचे‑नीचे रखते हुए,
  
• गुणक जितने खण्ड (टुकड़े) हों, उतने ही रूप में
  
• गुण्य को भी खण्डों के अनुसार गुणा किया जाता है,
  
• फिर उन सब परिणामों को जोड़कर अंतिम फल मिलता है।
  

हमारे स्तर पर सरल निष्कर्ष:

• गुण्य या गुणक (या दोनों) को खण्डों में बाँटते हैं,
  
• हर खण्ड से गुणा करते हैं,
  
• और सब परिणामों को जोड़ देते हैं।
  

उदाहरण ढांचा:

18 × 12

• 12 = 10 + 2 (खण्ड)
  
• 18 × 12 = 18 × 10 + 18 × 2
  

---

5. इष्ट गुणा (3.2.5)

---

सूत्र की पंक्ति:

“इष्टोन्युग्मेन गुणेन धनघ्नोऽभीष्टघ्नगुण्यान्वितो वाऽञ्जितो वा॥”

इसे सरल टुकड़ों में:

• इष्टः = इष्ट संख्या, हमारे अनुकूल, पास की आसान संख्या
  
• अन्युग्मेन गुणेन = दूसरी संख्या के साथ गुणे हुए (सहगुणन)
  
• धनघ्नः = धन (positive) संख्या से अभ्यास करने वाला
  
• अभीष्टघ्नगुण्य‑अन्वितः = इच्छित गुणांक से संयुक्त गुण्य
  
• अञ्जितः = सुधार किया हुआ, ठीक किया हुआ
  
• वा = या
  

सरल अर्थ:

• गुणा करते समय, किसी संख्या के पास की इष्ट (अनुकूल) संख्या से पहले गुणा करो,
  
• जैसे 49 की जगह 50, 98 की जगह 100,
  
• फिर जो अधिक या कम लिया गया है,
  
• उसका गुणा करके परिणाम में जोड़ या घटा कर
  
• सही उत्तर प्राप्त करो।
  

यही इष्ट गुणा की पूरी भावना है।

उदाहरण ढांचा:

49 × 18

• इष्ट = 50
  
• 50 × 18 = 900
  
• 49 की जगह 50 लेने से 1 × 18 ज्यादा हो गया
  
• असली उत्तर = 900 − 18 = 882
  

---

गुण्यान्त्यमङ्को गुणकेन हन्यादुत्सारितेनैवोपान्त्यमादीन्।

गुण्यस्त्वधोऽधो गुणिखण्डतुल्यस्तैः खण्डकैः संगुणितो युतो वा।

भवो गुणैः शुध्यति येन तेन लब्ध्या च गुण्यो गुणितैः फलं वा।

द्विधा भवेत् रूपविभाग एवम् स्थानैः पृथग्वा गुणितैः समस्तैः।

इष्टोन्युग्मेन गुणेन दनघ्नोऽभीष्टघ्नगुण्यान्वित वञ्जितो वा॥

बहुत अच्छा सवाल है – यही श्लोक पूरी “गुणा की पाँचों विधियाँ” का आधार है।
हम इसे बहुत आसान ढंग से, टुकड़ों में समझेंगे।

श्लोक:

गुण्यान्त्यमङ्को गुणकेन हन्यादुत्सारितेनैवोपान्त्यमादीन्।
गुण्यस्त्वधोऽधो गुणिखण्डतुल्यस्तैः खण्डकैः संगुणितो युतो वा।
भवो गुणैः शुध्यति येन तेन लब्ध्या च गुण्यो गुणितैः फलं वा।
द्विधा भवेत् रूपविभाग एवम् स्थानैः पृथग्वा गुणितैः समस्तैः।
इष्टोन्युग्मेन गुणेन धनघ्नोऽभीष्टघ्नगुण्यान्वितो वाऽञ्जितो वा॥

---

1. पहला भाग
   “गुण्यान्त्यमङ्को गुणकेन हन्यादुत्सारितेनैवोपान्त्यमादीन्।”
   

---

शब्दार्थ (सरल):

• गुण्य = जिसे गुणा करते हैं
  
• अन्त्यअङ्कः = अंतिम अंक (दाईं ओर का)
  
• गुणकेन = गुणक द्वारा (जिससे गुणा करते हैं)
  
• हन्यात् = गुणा करे
  
• उत्सारितेन एव = आगे बढ़ाकर (कैरी लेकर/ले जाते हुए)
  
• उपान्त्यम् आदीन् = उसके पहले वाले अंक आदि
  

सरल मतलब:

• गुण्य का सबसे दाहिना अंक गुणक से गुणा किया जाए।
  
• जो कैरी (उत्सार) निकले, उसे रखते हुए
  
• फिर उसके बाएँ वाले अंक को गुणा करो,
  
• इसी तरह क्रम से आगे बढ़ते जाओ।
  

हमारे लिए:

• यह सामान्य लंबवत (column) गुणा की पद्धति का संकेत है –
  जैसे हम कापी में नीचे‑नीचे लिखकर दाईं ओर से गुणा शुरू करते हैं।
  

यह भाग कुल मिलाकर “सामान्य गुणा” (long multiplication) के सिद्धांत को बताता है, जिस पर आगे की खास विधियाँ खड़ी हैं।

---

2. दूसरा भाग
   “गुण्यस्त्वधोऽधो गुणिखण्डतुल्यस्तैः खण्डकैः संगुणितो युतो वा।”
   

---

शब्दार्थ:

• गुण्यः = जिसे गुणा करते हैं
  
• तु = तो
  
• अधः अधः = नीचे‑नीचे (प्रत्येक पंक्ति में)
  
• गुणिखण्डतुल्यस्तैः = गुणक के खण्डों के समान रहने वाले
  
• खण्डकैः = खण्डों से, टुकड़ों से
  
• संगुणितः = गुणा किया हुआ
  
• युतः = जोड़ा हुआ
  
• वा = या
  

सरल अर्थ:

• गुणक (नीचे वाली संख्या) अगर खण्डों में बँटी हो,
  
• तो गुण्य को उन खण्डों के अनुसार
  नीचे‑नीचे रखकर,
  
• हर खण्ड से गुणा किया जाए,
  
• और सब परिणामों को जोड़ दिया जाए।
  

विधि से संबंध:

• यहाँ “गुणिखण्डतुल्यस्तैः खण्डकैः” से
  खण्डों द्वारा गुणा करने का सिद्धांत आता है →
  यहीं से “खण्ड गुणा” और “विभाग / खण्ड‑आधारित तरीकों” की प्रेरणा मिलती है।
  

सरल भाषा में:

• गुणक को टुकड़ों में बाँटो,
  
• गुण्य को हर टुकड़े से अलग‑अलग गुणा करो,
  
• सबको जोड़ दो → यही खण्ड/विभाग गुणा का भाव।
  

---

3. तीसरा भाग
   “भवो गुणैः शुध्यति येन तेन लब्ध्या च गुण्यो गुणितैः फलं वा।”
   

---

शब्दार्थ (मुख्य):

• भवः = अवशेष / शेष / दोष (error)
  
• गुणैः = गुणनफल या गुणकों द्वारा
  
• शुध्यति = शुद्ध हो जाता है, ठीक हो जाता है
  
• येन = जिससे
  
• तेन = उसी से
  
• लब्ध्या = भागफल से
  
• गुण्यः गुणितैः = गुण्य और गुणनफल के साथ
  
• फलं वा = या फल
  

यह भाग थोड़ा गहरा है, पर आसान रूप में:

• जो शेष/दोष (error) गुणा में आता है,
  
• वह उसी गुणक या भागफल से सुधारा जा सकता है।
  

यह विचार आगे “शोधन” (correction),
अनुपात, भाग और जटिल विधियों में काम आता है –
यहाँ आपके लिए बस इतना समझना ज़रूरी है कि:

• यदि हम कुछ ज्यादा या कम ले लेते हैं,
  
• तो उसी के अनुसार शोधन (correction) किया जाता है।
  

इसका स्पष्ट उपयोग आगे की विधियों जैसे इष्ट गुणा में दिखता है:

• पहले आसान इष्ट संख्या से गुणा,
  
• फिर जो ज्यादा/कम लिया, उसकी शुद्धि।
  

---

4. चौथा भाग
   “द्विधा भवेत् रूपविभाग एवम् स्थानैः पृथग्वा गुणितैः समस्तैः।”
   

---

आपने पहले ही शब्दार्थ बहुत अच्छा किया था।

शब्दार्थ:

• द्विधा भवेत् = दो तरह से हो सकता है
  
• रूपविभाग = रूपों में विभाजन
  
• एवम् = इस प्रकार
  
• स्थानैः = स्थानों (एकाई, दहाई, सैकड़ा) के अनुसार
  
• पृथक् वा = अलग‑अलग भी
  
• गुणितैः = गुणा करके
  
• समस्तैः = सबको जोड़कर
  

सरल अर्थ:

• संख्या का विभाजन दो प्रकार से हो सकता है –
  

1. रूपों में (रूपविभाग)
   
2. स्थानों के अनुसार
   

• इन भागों से अलग‑अलग गुणा करके
  
• और सभी परिणामों को जोड़कर
  
• पूरा गुणनफल प्राप्त किया जा सकता है।
  

विधियों से सीधा संबंध:

• “रूपविभाग” → रूप गुणा, विभाग गुणा
  (जैसे 15 = 10 + 5, 47 = 40 + 7)
  
• “स्थानैः पृथक्” → स्थान गुणा
  (जैसे 205 = 200 + 5, 14 = 10 + 4)
  

यानी यही एक पंक्ति “रूप गुणा + विभाग गुणा + स्थान गुणा” की जड़ है।

---

5. पाँचवाँ भाग
   “इष्टोन्युग्मेन गुणेन धनघ्नोऽभीष्टघ्नगुण्यान्वितो वाऽञ्जितो वा॥”
   

---

शब्दार्थ (सरल):

• इष्टः = इष्ट संख्या – हमारे अनुकूल, आसानी वाली संख्या
  
• अन्युग्मेन गुणेन = दूसरे गुणक के साथ मिलाकर गुणा
  
• धनघ्नः = धन (positive संख्या) से गुणा करने वाला
  
• अभीष्टघ्न‑गुण्य‑अन्वितः = इच्छित गुणांक से संयुक्त गुण्य
  
• अञ्जितः = संशोधित, ठीक किया हुआ
  
• वा = या
  

आसान भाषा में अर्थ:

• गुणा करते समय, किसी संख्या की जगह उसके पास की आसान इष्ट संख्या लेकर
  दूसरी संख्या से गुणा कर सकते हैं।
  
• बाद में, जो ज्यादा या कम लिया गया है,
  उसी के अनुसार शोधन (जोड़ या घटाकर)
  सही गुणनफल प्राप्त करना चाहिए।
  

यही भाव सीधे “इष्ट गुणा” की विधि है।

उदाहरण (जो हमने साथ किया था):

49 × 18:

• इष्ट संख्या: 50 (49 के पास आसान)
  
• 50 × 18 = 900
  
• लेकिन 50, 49 से 1 ज्यादा → 1 × 18 ज्यादा हो गया
  
• शोधन: 900 − 18 = 882
  
• तो 49 × 18 = 882
  

इसे ही श्लोक की भाषा में कहा गया:
इष्ट संख्या से गुणा करो, फिर शोधन करके सही फल पाओ।

---

4.3.2 श्लोक:

अथ स्थाय्योन्नवर्गौ द्विगुणान्यनिघ्नाः
स्वस्वोपरिष्टाच्च तथापरेऽङ्काः।
तत्समान्यमुत्सार्य पुनः राशिम्॥

यह “किसी दो-अंकीय संख्या का वर्ग निकालने की विधि” का सूत्र है। एक‑एक शब्द का आसान अर्थ देखते हैं:

1. अथ स्थाय्योन्नवर्गौ
   

• स्थायी = जो अंक स्थिर है (दहाई का अंक)
  
• उपन = उसके ऊपर/साथ वाला अंक (इकाई का अंक)
  
• वर्गौ = दोनों का वर्ग
  

भाव: सबसे पहले दहाई और इकाई दोनों अंकों का वर्ग लो।

2. द्विगुणान्यनिघ्नाः
   

• द्विगुण = दो गुना
  
• अनिघ्नाः = गुणे हुए
  

भाव: फिर दोनों अंकों का दो गुना गुणन करो (यानी: 2 × (दहाई का अंक) × (इकाई का अंक))।

3. स्वस्वोपरिष्टाच्च तथापरेऽङ्काः
   

• स्वस्व = अपने‑अपने
  
• उपरिष्टात् = ऊपर, उसके बाद
  
• अपरेऽङ्काः = जो आगे के अंक हैं
  

भाव: जो-जो संख्याएँ मिली हैं (वर्ग, फिर बीच का पद, फिर वर्ग), उन्हें क्रम से एक के बाद एक लिखो।

4. तत्समान्यमुत्सार्य पुनः राशिम्
   

• तत्सामान्यम् = जो समान (कॅरी वाले) भाग हैं
  
• उत्सार्य = ऊपर चढ़ाकर / जोड़कर
  
• पुनः राशिम् = फिर अंतिम संख्या (राशि) बनाओ
  

भाव: जो कॅरी बनता है, उसे आगे के अंक में जोड़कर अंतिम संख्या (वर्ग) बना लो।

संपूर्ण सरल भावार्थ:
“किसी दो-अंकीय संख्या का वर्ग निकालने के लिए – पहले दोनों अंकों के वर्ग लो, फिर दोनों अंकों का दो गुना गुणन करो, इन सबको क्रम से लिखो, जो कॅरी बने उसे आगे जोड़कर अंतिम वर्ग (संख्या) प्राप्त करो।”

अब एक छोटा अभ्यास:
मान लो संख्या 23 है।
दहाई का अंक = 2, इकाई का अंक = 3
पहला कदम: “दोनों का वर्ग” –
आप बताइए: 2² और 3² कितने होंगे? (सिर्फ दो संख्याएँ लिखिए)

ठीक, अब बिना घुमाए, सीधे फटाफट पूरा तरीका और अर्थ दे रहा हूँ।

श्लोक:  

अथ स्थाय्योन्नवर्गौ द्विगुणान्यनिघ्नाः  

स्वस्वोपरिष्टाच्च तथापरेऽङ्काः।  

तत्समान्यमुत्सार्य पुनः राशिम्॥

सार अर्थ (संक्षेप में):  

यह दो-अंकीय संख्या का वर्ग निकालने का नियम है।

विधि (दो-अंकीय संख्या AB के लिए, जैसे 23, 47 आदि):

1) स्थाय्योन्नवर्गौ  

   – A = दहाई का अंक, B = इकाई का अंक  

   – पहले A² और B² निकालो।

2) द्विगुणान्यनिघ्नाः  

   – बीच का पद = 2AB (दोनों अंकों का 2 गुना गुणन)।

3) स्वस्वोपरिष्टाच्च तथापरेऽङ्काः  

   – तीन पद एक क्रम में लिखो:  

     A², 2AB, B²  

   – जरूरत हो तो अंकों को दो-दो डिजिट में मानकर लिखो (जैसे 4 को 04)।

4) तत्समान्यमुत्सार्य पुनः राशिम्  

   – बीच-बीच से जो carry बने, उसे आगे जोड़कर अंतिम संख्या बनाओ – यही AB का वर्ग है।

उदाहरण 23² (झटपट):

– A = 2, B = 3  

– A² = 4 → 04 मानेंगे  

– B² = 9 → 09  

– 2AB = 2 × 2 × 3 = 12  

अब क्रम से लिखो: 04 | 12 | 09  

– दाएँ से: 09  

– बीच का 12: 2 नीचे, 1 carry  

– 04 + 1 = 05  

अंतिम उत्तर: 23² = 529

इसी नियम को श्लोक ने compact रूप में कहा है –  

पहले दोनों अंकों के वर्ग, फिर 2AB, फिर carry सम्हाल कर योग = वर्ग।  

अगर चाहो तो मैं यही प्रक्रिया 47² या आपकी पसंद की किसी संख्या पर भी इसी तरह बिना व्याख्या के सिर्फ steps में लिख सकता हूँ।

ठीक, सिर्फ काम की चीज़ लिखता हूँ – बिना अतिरिक्त समझाने के।

तीन-अंकीय संख्या 547 के वर्ग का “फॉर्मूला जैसा” स्टेप:

मानो संख्या = 547 = 54 | 7  

तो:

1) X = 54, Y = 7  

2) X² = 54² = 2916  

3) Y² = 7² = 49  

4) बीच का पद = 2XY  

   2XY = 2 × 54 × 7 = 756  

अब स्थान के हिसाब से लिखें:

– X² = 2916 → 29160000  

– 2XY = 756 → 0075600  

– Y² = 49 → 000049  

जोड़:

29160000  

+  0075600  

+    000049  

= 29925649  

अतः:  

547² = 29925649

ऊपर जो सूत्र है:

खण्डद्वयस्याभिहतिर्द्विगुणिता तत्त्वद्वर्गैः संयुता कृतिरिति।

इसका मतलब है:
“किसी संख्या का वर्ग निकालना हो, तो पहले उसे दो भागों में बाँटो;
दोनों भागों का गुणन करके उसे द्विगुणित करो;
फिर दोनों भागों के वर्ग लेकर उसमें जोड़ दो —
जो संख्या मिले, वही मूल संख्या का वर्ग है।”

यानी शुद्ध बीजगणित में यही बात है:
यदि संख्या  को  मानें, तो

अब जो 17 का उदाहरण दिया है, उसे स्टेप से देखो:

1. हमें 17 का वर्ग करना है।
2. 17 को दो भागों में बाँटा:

3. दोनों खंडों का गुणन कर के उसे दुगुना किया:

4. दोनों खंडों का वर्ग लेकर जोड़ा:

5. अब सूत्र के अनुसार
   “दोनों खंडों के द्विगुण गुणनफल को दोनों खंडों के वर्ग के योग में जोड़ो”:

यही है खण्डद्वय विधि:
संख्या को दो भाग करो →  निकालो →  जोड़ो → पूरा वर्ग मिल जाता है।

बहुत अच्छा, अब सीधे 4.3.4 वाले सूत्र की व्याख्या करते हैं।

सूत्र:

इष्टेन युग्माशिवधः कृति: स्यादिष्टस्य वर्गेण समानितो वा।

इसे दो भागों में समझो:

1. “इष्टेन युग्माशिवधः कृतिः स्यात्”

• इष्टेन = किसी मनचाही (सुविधाजनक) संख्या से
• युग्म‑अशि‑वधः = “जोड़कर, घटाकर, गुणा करके”
• कृतिः स्यात् = वर्ग प्राप्त होता है

भावार्थ (सरल):
किसी संख्या का वर्ग निकालने के लिए, उसे किसी सुविधाजनक इष्ट संख्या से जोड़कर या घटाकर, फिर उनका गुणन करके भी वर्ग पाया जा सकता है।

2. “इष्टस्य वर्गेण समानितो वा”

• इष्टस्य वर्गेण = उस इष्ट संख्या के वर्ग के द्वारा
• समानितः = सम कर के / ठीक करके
• वा = या

भावार्थ:
फिर उस इष्ट संख्या के वर्ग को जोड़‑घटा कर, परिणाम को ठीक किया जाता है; इस तरह मूल संख्या का वर्ग मिल जाता है।

बीजगणितीय रूप से यही बात है:

यदि कोई संख्या  है और इष्ट संख्या  ली, तो

या तो  लेकर

या  लेकर

यानी:
“इष्ट” संख्या के आस‑पास की संख्या का वर्ग, इष्ट के वर्ग और दोनों के जोड़‑घटाव व गुणन से निकाला जा सकता है।

(जहाँ B इष्ट अंक है)

मतलब क्या?

• A = जिसकी वर्ग निकालना है
• B = इष्ट (सुविधाजनक) संख्या

सूत्र कहता है:
किसी संख्या A का वर्ग ऐसे भी निकाल सकते हैं:

1. पहले (A + B) और (A – B) का गुणन करो
2. फिर उसमें B² जोड़ दो

जो परिणाम मिलेगा, वही A² होगा।

बीजगणित से जाँच लो:

अब अगर इसमें B² जोड़ दो:

यही तुम्हारे सूत्र की सच्चाई है।

अब 16 के लिए इसी से फटाफट देखते हैं:

• A = 16
• इष्ट B = 2 (ताकि 16 ± 2 आसान हों)

तो:

• A + B = 18
• A – B = 14
• B² = 4

सूत्र लगाओ:

18 × 14 = 252
252 + 4 = 256

यानी 16² = 256 — वही जो चाहिए था।

तो:

• “इष्टेन युग्माशिवधः…” वाला संस्कृत सूत्र
• और यह

---

---

बीजगणित: परिभाषा, उद्भव और विकास

लघु प्रश्नोत्तर

1. अव्यक्त गणित किसे कहते हैं?

उत्तर: C. बीजगणित

बीजगणित को अव्यक्त गणित कहा जाता है क्योंकि इसमें अज्ञात राशियों को अक्षरों द्वारा प्रदर्शित किया जाता है। "अव्यक्त" शब्द का अर्थ है – जो स्पष्ट रूप से व्यक्त न हो। जबकि अंकगणित को व्यक्त गणित कहा जाता है क्योंकि इसमें निश्चित संख्याओं का प्रयोग होता है।

2. अलजब्र किस भाषा का प्रतीक है?

उत्तर: B. अरबी भाषी

"अलजब्र" (Al-Jabr) एक अरबी भाषी शब्द है। यह शब्द अरब गणितज्ञ मुहम्मद बिन मूसा अल-खारिज़्मी द्वारा 825 ई. के दौरान लिखी गई पुस्तक "अल्जब्रुल मुकावला" से आया है। "अलजब्र" का अर्थ है "समीकरण" या "पूर्ण करना"।

3. बीजगणित का प्रादुर्भाव कहाँ से हुआ?

उत्तर: C. भारत

बीजगणित का उद्भव और विकास भारत में हुआ। भारतीय गणितज्ञों जैसे आर्यभट (476 ई.), ब्रह्मगुप्त (598-668 ई.), और भास्कराचार्य (12वीं शताब्दी) ने बीजगणित को विकसित किया। बाद में यह ज्ञान अरब के माध्यम से यूरोप तक पहुँचा।

4. बीजगणित के सांकेतिक स्वरूप कौन से हैं?

उत्तर: B और C (क-ख-ग, और a-b-c)

बीजगणित में अज्ञात राशियों को प्रदर्शित करने के लिए सांकेतिक स्वरूप का प्रयोग किया जाता है। भारतीय गणित में देवनागरी अक्षरों (क-ख-ग) का प्रयोग होता रहा है, जबकि अंतर्राष्ट्रीय पद्धति में रोमन अक्षर (a-b-c) का प्रयोग होता है।

5. समीकरण का वास्तविक अर्थ कौन सा है?

उत्तर: A. समीकरण – जो दो वस्तुओं को समान अथवा तुल्य बताता है।

समीकरण (Equation) का अर्थ है दो गणितीय व्यंजकों को एक समान स्थापित करना। यह दो राशियों या व्यंजकों के बीच समानता दर्शाता है। उदाहरण: 2x + 3 = 7

---

दीर्घ प्रश्न

1. बीजगणित के उद्भव एवं विकास का उल्लेख कीजिए

वैदिक काल में बीजगणित की नींव

बीजगणित की जड़ें वैदिक काल (1500 ई. पूर्व) तक जाती हैं। भारतीय गणितज्ञों ने वैदिक ग्रंथों और शुल्व सूत्रों में गणितीय समस्याओं के समाधान के संकेत दिए हैं। "शुल्व सूत्रों" में यज्ञों के लिए वेदियों के निर्माण से संबंधित ज्यामितीय समस्याओं का वर्णन है।

बौधायन (लगभग 800-700 ई. पूर्व) के सूत्रों में द्विघात समीकरणों का प्रमाण मिलता है। उन्होंने पाइथागोरस प्रमेय को समकोण त्रिभुज के माध्यम से व्यक्त किया:

यदि भुजा क = 3 और भुजा ख = 4, तो करण (कर्ण) = √(3² + 4²) = 5

जैन गणित और बीजगणित

जैन स्थानांगसूत्र (350 ई. पूर्व) में बीजगणित के विभिन्न रूपों का उल्लेख है:

• यावत्तावत् (सरल समीकरण)
• वर्ग (द्विघात समीकरण)
• घन (त्रिघात समीकरण)
• वर्गवर्ग (चतुर्घात समीकरण)
• विकल्प (क्रमचय और संचय)

शास्त्रीय काल में विकास

आर्यभट (476 ई.) ने अपनी पुस्तक "आर्यभटीय" में बीजगणित के प्रमुख तत्वों का वर्णन किया। वे बीजचतुष्टय (चार प्रकार के समीकरण) से परिचित थे। उनका एक महत्वपूर्ण योगदान रैखिक अनिर्धारित समीकरणों का समाधान था।

ब्रह्मगुप्त (598-668 ई.) ने अपने ग्रंथ "ब्रह्मस्फुटसिद्धांत" में:

• समीकरणों का वर्गीकरण किया
• शून्य के नियम स्थापित किए
• कुट्टक विधि का विस्तार किया
• द्विघात समीकरणों के समाधान दिए

भास्कराचार्य (1114-1185 ई.) ने अपनी पुस्तक "बीजगणितम्" में:

• बीजगणित को एक स्वतंत्र विषय के रूप में स्थापित किया
• चक्रवाल विधि (Chakravala method) का विस्तार किया
• करणी (surds) का विस्तृत अध्ययन दिया
• अनेक प्रकार के समीकरणों के समाधान प्रस्तुत किए

बीजगणित शब्द का उद्भव

"बीजगणित" शब्द संस्कृत के दो शब्दों से बना है:

• बीज = मूल, आधार, बीज
• गणित = गणना, विज्ञान

इसका शाब्दिक अर्थ है "मूल गणना की विद्या"।

---

2. भारतीय गणित का अरब एवं यूनानी गणित पर प्रभाव

भारतीय गणित का अरब में प्रभाव

8वीं-9वीं शताब्दी में प्रसार:

• भारतीय गणितज्ञों के ग्रंथों का अरबी भाषा में अनुवाद किया गया
• आर्यभट और ब्रह्मगुप्त के कार्यों को अरब विद्वानों ने अध्ययन किया
• अरब गणितज्ञ मुहम्मद बिन मूसा अल-खारिज़्मी (780-850 ई.) ने भारतीय गणित पर आधारित पुस्तक "अल्जब्रुल मुकावला" लिखी

अल-खारिज़्मी का योगदान:

• उन्होंने भारतीय दशमलव प्रणाली को अरब में लोकप्रिय बनाया
• शून्य की अवधारणा को अरब में प्रचारित किया
• बीजगणित को एक व्यवस्थित विज्ञान के रूप में संगठित किया

भारतीय गणित का यूनानी गणित पर प्रभाव

यूनानी गणितज्ञ डायोफंटस (लगभग 330 ई.) के "अरिथमेटिका" में मिलने वाले बीजगणितीय नियम भारतीय प्रभाव के प्रमाण हैं। गणितीय इतिहासकार डॉ. ई. काजोरी का मानना है कि डायोफंटस के बीजगणितीय नियम भारतीय गणितज्ञों से ही प्राप्त हुए थे।

यूरोप तक प्रभाव

11वीं शताब्दी में:

• इतालवी व्यापारी लियोनार्डो ने अल-खारिज़्मी की पुस्तक को इटली लाया
• चेस्टर के राबर्ट (1140 ई. के आसपास) ने इसका लैटिन में अनुवाद किया

16वीं शताब्दी में:

• यूरोप के गणितज्ञों ने भारतीय और अरबी पद्धतियों को अपनाया
• फ्रांकोइस विएते ने आधुनिक प्रतीकात्मक बीजगणित का विकास किया

अन्य क्षेत्रों पर प्रभाव

• चीन और जापान: भारतीय गणितीय प्रक्रियाएं चीनी गणितज्ञों तक पहुँचीं
• फारस: फारसी विद्वानों ने भारतीय गणित को अपनाया

---

3. बीजगणित की विधियों का उल्लेख

विधि 1: शून्य सिद्धांत (Zero Theory)

भास्कराचार्य ने शून्य के नियमों को स्पष्ट किया:

शून्य से संबंधित नियम:

• क + 0 = क (किसी संख्या में शून्य जोड़ने से संख्या अपरिवर्तित रहती है)
• क – 0 = क (किसी संख्या से शून्य घटाने से संख्या अपरिवर्तित रहती है)
• क × 0 = 0 (शून्य से गुणा करने पर परिणाम शून्य होता है)
• क ÷ 0 = ∞ (किसी संख्या को शून्य से भाग देने पर अनंत प्राप्त होता है)
• 0 – क = -क (शून्य से किसी धन संख्या को घटाने पर ऋण संख्या मिलती है)

विधि 2: समीकरण विधि (Equation Method)

समीकरण की परिभाषा: जो दो वस्तुओं को समान अथवा तुल्य बताता है।

समीकरणों का वर्गीकरण:

1. एकचर समीकरण (One variable equations) – जिसमें एक अज्ञात राशि हो

• उदाहरण: 2x + 5 = 13

2. बहुचर समीकरण (Multiple variable equations) – जिसमें अनेक अज्ञात राशियाँ हों

• उदाहरण: 2x + 3y = 13

3. उच्च घात समीकरण (Higher degree equations) – द्वितीय, तृतीय आदि घातों के समीकरण

• द्विघात: x² + 5x + 6 = 0
• त्रिघात: x³ + 2x² – x – 2 = 0

4. भादित समीकरण (Mixed equations) – कई अज्ञातों के गुणनफल वाले

विधि 3: कुट्टक विधि (Indeterminate Equation Method)

परिभाषा: यदि किसी दी हुई संख्या को किसी अज्ञात संख्या से गुणा करें, फिर इसमें कोई अन्य संख्या घटाएँ या जोड़ें, और फिर किसी दिए गए भाजक से भाग दें जिससे अंत में शून्य शेष बचे, तो उस गुणक को कुट्टक कहते हैं।

कुट्टक विधि का रूप: ax + b ≡ c (mod m)

ऐतिहासिक महत्व:

• आर्यभट ने इस विधि को पहली बार व्यवस्थित रूप से समाधान दिया
• ब्रह्मगुप्त ने इसका विस्तार किया
• भास्कराचार्य ने कुट्टकाध्याय में विस्तृत व्याख्या दी

विधि 4: चक्रवाल विधि (Cyclic Method)

यह विधि x² – Dy² = 1 जैसे पेल समीकरणों को हल करने के लिए उपयोग होती है।

विशेषताएँ:

• यह एक पुनरावर्ती (iterative) विधि है
• ब्रह्मगुप्त के समय में इसका संक्षिप्त रूप ज्ञात था
• भास्कराचार्य ने इसे पूर्ण विकसित रूप दिया

विधि 5: करणी विधि (Surd Method)

करणी की परिभाषा: जिस राशि का पूरा मूल न मिले, उसे करणी कहते हैं।

उदाहरण: √2, √3, √5 आदि

करणी के प्रकार:

• सरल करणी: √a
• मिश्र करणी: √a + √b

---

4. समीकरण एवं कुट्टक विधि क्या है, स्पष्ट कीजिए

समीकरण (Equation)

परिभाषा: समीकरण गणित की वह कथन है जो दो गणितीय व्यंजकों के बीच समानता दर्शाती है।

समीकरण का सामान्य रूप:

• एक पक्ष = दूसरा पक्ष

समीकरण के उदाहरण:

1. सरल रैखिक समीकरण: 2x + 3 = 7

• हल: x = 2

2. द्विघात समीकरण: x² – 5x + 6 = 0

• हल: x = 2 या x = 3

समीकरण हल करने की विधि:

• दोनों पक्षों में समान संक्रियाएँ करें
• अज्ञात राशि को अलग करें
• समीकरण को संतुलित रखें

समीकरण का महत्व:

• वास्तविक समस्याओं का समाधान
• अज्ञात राशियों का पता लगाना
• गणितीय संबंधों की खोज

कुट्टक विधि (Indeterminate Equation Method)

परिभाषा: कुट्टक विधि से उन समीकरणों का समाधान किया जाता है जिनमें अनंत समाधान संभव होते हैं या जिनमें एक से अधिक अज्ञात राशियाँ होती हैं।

कुट्टक का गणितीय रूप:

• ax + by = c

कुट्टक के उदाहरण:

उदाहरण 1: 3x + 5y = 23

• संभव समाधान: (x=4, y=2.2), (x=6, y=1), आदि

उदाहरण 2: 7x ≡ 1 (mod 5)

• इसका अर्थ है: 7x को 5 से भाग देने पर शेष 1 बचे

कुट्टक विधि के चरण:

1. समीकरण का रूप: ax + by = c

2. अनुक्रमिक विभाजन: a और b का अनुक्रमिक भाग (successive division) करें

3. संख्याओं को पीछे की ओर रखें: प्राप्त भागफलों को वापस प्रतिस्थापित करें

4. समाधान प्राप्त करें: x और y के विशेष समाधान निकालें

5. सामान्य समाधान:

• x = x₀ + (b/gcd(a,b))×t
• y = y₀ – (a/gcd(a,b))×t
• (जहाँ t कोई पूर्णांक है)

कुट्टक विधि का महत्व:

1. भारतीय गणित में प्राचीनता:

• आर्यभट ने इसे पहली बार व्यवहार में लाया
• यह विधि 500 ई. से पहले के गणितज्ञों के पास ज्ञात थी

2. अरब और यूरोप में प्रभाव:

• अल-खारिज़्मी ने भारतीय पद्धति का अनुसरण किया
• यूरोपीय गणितज्ञों ने इसे 16वीं शताब्दी में पुनः खोजा

3. आधुनिक अनुप्रयोग:

• संख्या सिद्धांत (Number Theory)
• क्रिप्टोग्राफी (Cryptography)
• कंप्यूटर विज्ञान

कुट्टक और समीकरण में अंतर:

विशेषता	समीकरण	कुट्टक
अज्ञात	एक या अधिक	आमतौर पर दो या अधिक
समाधान	सीमित (प्राय: एक)	अनंत
उदाहरण	2x = 10	2x + 3y = 10
घात	कोई भी	प्रायः प्रथम घात
उपयोग	सामान्य समस्याएँ	विशेष समस्याएँ

व्यावहारिक उदाहरण

उदाहरण: एक व्यापारी के पास कुछ 5 रुपये और कुछ 7 रुपये के सिक्के हैं। यदि कुल 35 रुपये हों, तो प्रत्येक प्रकार के कितने सिक्के हो सकते हैं?

समीकरण: 5x + 7y = 35

संभव समाधान:

• x = 7, y = 0 (7 पाँच रुपये के सिक्के)
• x = 0, y = 5 (5 सात रुपये के सिक्के)
• x = 2, y = 2.86… (संभव नहीं, क्योंकि आधा सिक्का नहीं हो सकता)

---

बीजगणित की महत्वपूर्ण परिभाषाएँ

बीजगणित: वह गणित जिसमें अक्षरों की सहायता से गणितीय समस्याओं का हल निकाला जाता है।

अव्यक्त गणित: जिसमें अज्ञात राशियों को प्रतीकों से दर्शाया जाता है।

व्यक्त गणित (अंकगणित): जिसमें निश्चित संख्याओं का प्रयोग होता है।

अलजब्र: अरबी भाषा में समीकरण का पर्यायवाची शब्द।

कुट्टक: बीजगणित में प्रथम घात के अनिर्धारित विश्लेषण को कहा जाता है।

करणी: वह राशि जिसका पूरा मूल न मिले।

---

बीजगणित का विश्व में प्रभाव

1. वैज्ञानिक क्रांति: बीजगणित ने आधुनिक विज्ञान की नींव तैयार की
2. प्रौद्योगिकी विकास: कंप्यूटर और डिजिटल तकनीक में अनिवार्य
3. अर्थशास्त्र: व्यापार और वित्त में समीकरणों का व्यापक उपयोग
4. चिकित्सा: औषधि विज्ञान में गणितीय गणनाएँ

---

निष्कर्ष

भारतीय गणितज्ञों का बीजगणित के विकास में योगदान संसार में अतुलनीय है। आर्यभट, ब्रह्मगुप्त और भास्कराचार्य जैसे महान गणितज्ञों ने न केवल बीजगणित के सिद्धांतों को विकसित किया, बल्कि इसे एक व्यवस्थित विज्ञान के रूप में प्रस्तुत किया। यह ज्ञान अरब के माध्यम से यूरोप तक पहुँचा और आधुनिक गणित की नींव बना। इस प्रकार, भारतीय बीजगणित विश्व गणितीय परंपरा का एक महत्वपूर्ण अंग है।

---

CVG- 003

---

लघु प्रश्नोत्तर (उत्तर सहित)

1. भास्कराचार्य की कौन-सी रचना है?
 उत्तर:
 B. लीलावती
स्पष्टीकरण:
 'लीलावती' भास्कराचार्य की प्रसिद्ध गणितीय ग्रंथ है जिसमें अंकगणित के सरल से जटिल प्रश्नों को हल किया गया है।

---

2. पंचसिद्धांतिका के पांच सिद्धांत कौन-से हैं?
 उत्तर:
 C. पैतामह, वाशिष्ठ, रोमक, पॉलिश, सौर
स्पष्टीकरण:
 वराहमिहिर द्वारा रचित 'पंचसिद्धांतिका' में खगोलशास्त्र के ये पाँच प्रमुख सिद्धांत सम्मिलित हैं।

---

3. वराहमिहिर की कौन-सी रचना है?
 उत्तर:
 A. बृहत्संहिता
स्पष्टीकरण:
 वराहमिहिर की 'बृहत्संहिता' संस्कृत साहित्य की महान खगोल एवं भविष्यवाणी संबंधी रचना है।

---

4. 'खं' का अर्थ क्या है?
 उत्तर:
 B. शून्य
स्पष्टीकरण:
 'खं' शब्द का प्रयोग प्राचीन भारतीय गणित में 'शून्य' (0) के लिए किया जाता था।

---

5. अव्यक्त राशि किसे कहते हैं?
 उत्तर:
 B. अमूर्त संख्या
स्पष्टीकरण:
 अव्यक्त राशि का अर्थ है ऐसी संख्या या राशि जिसे प्रत्यक्ष रूप में ज्ञात नहीं किया जा सकता—इसे अमूर्त संख्या कहा जाता है।

---

दीर्घ प्रश्नोत्तर

3. वराहमिहिर का भारतीय गणित में क्या योगदान रहा? उल्लेख करें।
 उत्तर:
 वराहमिहिर ने भारतीय गणित और ज्योतिष के क्षेत्र में उल्लेखनीय योगदान दिया। उन्होंने 'बृहत्संहिता', 'बृहत्जातक' और 'पंचसिद्धांतिका' जैसे महत्वपूर्ण ग्रंथों की रचना की। पंचसिद्धांतिका में उन्होंने प्राचीन भारतीय खगोलशास्त्र के पांच प्रमुख सिद्धांतों का विवेचन किया। बृहत्संहिता में कालगणना, ज्योतिष, ग्रह-गणना, वास्तु आदि विषयों का विस्तार से वर्णन किया। उनकी यह कृतियाँ गणित को ज्योतिष और व्यावहारिक जीवन से जोड़ती हैं।

---

4. भास्कराचार्य का किस प्रकार भारतीय बीजगणित में योगदान रहा? वर्णन करें।
 उत्तर:
 भास्कराचार्य (भास्कर द्वितीय) ने बीजगणित (Algebra) को भारत में एक नई ऊँचाई दी। उन्होंने लीलावती, बीजगणित, गणिताध्याय तथा गोलाध्याय आदि भागों में गणितीय सिद्धांतों को सुव्यवस्थित किया। भास्कराचार्य ने अपूर्णांक, ऋणात्मक संख्या, शून्य और अनंत, समीकरण हल करने की विधियाँ तथा चक्रवाल विधि का प्रतिपादन किया। उनके कार्य ने न केवल भारत, बल्कि पूरे गणित-जगत को प्रभावित किया।

---

5. श्रीराम अभ्यंकर के गणित में योगदान का उल्लेख कीजिए।
 उत्तर:
 श्रीराम शंकर अभ्यंकर एक प्रसिद्ध भारतीय-अमेरिकी गणितज्ञ रहे। उनका योगदान समष्टि ज्यामिति (Algebraic Geometry) तथा सिंगुलैरिटी सिद्धांत (Singularity Theory) में महत्वपूर्ण रहा। ‘Abhyankar’s conjecture’ तथा ‘Abhyankar’s lemma’ उनके नाम से प्रसिद्ध हैं। वे गणित के उच्च अध्ययन और शोध कार्यों में प्रेरणा का स्रोत बने।

---

3.  वराहमिहिर का भारतीय गणित में योगदान

अवधारणा व ऐतिहासिक भूमिका:
  भारत के प्रसिद्ध गणितज्ञ एवं ज्योतिषाचार्य थे। उनका योगदान गणित, खगोलशास्त्र और ज्योतिष तीनों क्षेत्रों में अद्वितीय है। उनकी प्रमुख रचनाएँ हैं—बृहत्संहिता, पंचसिद्धांतिका, बृहत्जातक।

मुख्य योगदान:

• पंचसिद्धांतिका: इस ग्रंथ में उन्होंने भारतीय खगोलशास्त्र के पाँच ज्ञानमार्गों—पैतामह, वाशिष्ठ, रोमक, पॉलिश, और सौर सिद्धांत का गहन विवेचन किया। इसमें पुराने सिद्धांतों का संश्लेषण और तुलना साथ-साथ प्रस्तुत की गई है।
  
• बृहत्संहिता: इसमें गणित, वास्तु, जलविज्ञान, नक्षत्रशास्त्र, ज्योतिष, कालगणना आदि के सूत्र प्रदान किए गए हैं।
  
• गणित में नवाचार: वराहमिहिर ने त्रिकोणमिति, गणना-पद्धतियाँ, विभाजन-सिद्धांतों तथा प्रत्यक्ष गणना को विज्ञान के अन्य क्षेत्रों से जोड़ा।
  
• प्रभाव: उनकी कृतियों ने आगे चलकर गणितीय अनुसंधान, खगोलगणना और भविष्यवाणी विज्ञान को परिष्कृत किया। उनके सूत्र आज भी ज्योतिष एवं गणित के शिक्षण-साहित्य में सम्मिलित हैं।
  

निष्कर्ष:
 वराहमिहिर ने भारत में गणितीय चिंतन एवं वैज्ञानिक पद्धति को प्रगाढ़ किया, जिससे भारतीय ज्योतिष और गणना में नयापन आया।

---

4. भास्कराचार्य का भारतीय बीजगणित में योगदान

परिचय:
 भास्कराचार्य (भास्कर द्वितीय, 1114–1185) भारत के सर्वश्रेष्ठ गणितज्ञ और खगोलशास्त्री के रूप में विख्यात हैं। उनका सबसे प्रसिद्ध ग्रंथ है ‘लीलावती’, जिसमें बीजगणित व अंकगणित के विविध विषयों को व्याख्यायित किया गया है।

मुख्य योगदान:

• ‘लीलावती’ ग्रंथ: समस्या-आधारित प्रस्तुतिकरण जिसमें दैनिक जीवन से गणना, विभाजन, अनुपात, श्रेणी, गुणा-भाग आदि के सवाल हल किए गए हैं।
  
• बीजगणित (Algebra): समीकरण हल करने की ‘चक्रवाल विधि’, द्विघात एवं अन्य समीकरणों को हल करने की योजनाबद्ध विधियाँ।
  
• शून्य, ऋणात्मक एवं अपूर्णांक संख्याएँ: इनका सहज प्रयोग एवं गणना।
  
• गोलाध्याय व गणिताध्याय: गणित के विविध विषयों को सुव्यवस्थित किया।
  
• अनंत व कलन: अनंत श्रेणी का विश्लेषण, कलन की पूर्वपीठिका।
  

विशिष्टता:
 उनकी पुस्तकों की संवाद शैली, गूढ़-से-सरल उदाहरण, और व्यावहारिक दृष्टिकोण ने गणित के शिक्षण को सभी के लिये सुलभ एवं रुचिकर बना दिया।

निष्कर्ष:
 भास्कराचार्य ने बीजगणितीय विचार और उसकी विधियों को जनसामान्य तक पहुँचाया, जिससे भारतीय गणित विज्ञान में क्रांति आई।

---

5. श्रीराम अभ्यंकर का गणित में योगदान

परिचय:
 श्रीराम शंकर अभ्यंकर (1930–2012) भारतीय-अमेरिकन गणितज्ञ थे, जिन्होंने आधुनिक बीजगणितीय ज्यामिति (Algebraic Geometry) एवं सिंगुलैरिटी सिद्धांत में क्रांतिकारी कार्य किए।

मुख्य योगदान:

• Abhyankar's Conjecture: गणितीय बीजगणितीय भूमिकाओं एवं सतहों के विस्तार पर उनका प्रमेय, जो मोटे तौर पर क्षेत्र विस्तार एवं सिंगुलैरिटी जाँचता है।
  
• Abhyankar’s Lemma: बीजगणित के उच्च अध्ययन में अत्यंत उपयोगी प्रमेय।
  
• शोध एवं प्रेरणा: उन्होंने भारतीय एवं वैश्विक गणित समुदाय में उच्च स्तर पर प्रेरणा दी, अनेक शिक्षाविदों और शोधार्थियों को सक्रिय किया।
  
• ज्ञान-प्रसार: Purdue University (USA) में पढ़ाते हुए उन्होंने गणित में अनुसंधान हेतु पीढ़ियों को प्रेरित किया।
  

निष्कर्ष:
 अभ्यंकर का शोध आधुनिक बीजगणितीय ज्यामिति, सतहों के अध्ययन और सिंगुलैरिटी सिद्धांत को नई ऊँचाई तक ले गया, जिससे उनका नाम वैश्विक गणितिक विमर्श में सम्मानपूर्वक लिया जाता है।

---

1.5 अभ्यास हेतु प्रश्न – विस्तृत समाधान

अति लघु उत्तरीय प्रश्न (Short Answer Questions)

---

प्रश्न 1: एक लाख संख्या के लिए संस्कृत में किस शब्द का प्रयोग किया गया है?

उत्तर: लक्ष (Lakṣa)

विस्तृत व्याख्या:
संस्कृत गणितीय ग्रंथों में एक लाख (100,000) संख्या को लक्ष] या लक्षम्] कहा जाता है। यह शब्द प्राचीन संख्या प्रणाली में एक महत्वपूर्ण मापदंड है।

तुलनात्मक तालिका:

संख्या (अंकों में)	संस्कृत शब्द	आधुनिक नाम
10	दश	दस
100	शत	सौ
1,000	सहस्र	हज़ार
100,000	लक्ष	लाख
1,000,000	प्रयुत	दस लाख

---

प्रश्न 2: 'कुट्टक गणित' का नामकरण किस गणितज्ञ के द्वारा किया गया?

उत्तर: भास्कराचार्य (Bhaskara II)

विस्तृत व्याख्या:
'कुट्टक' (Kuttaka) शब्द संस्कृत में 'कुट्ट' से बना है जिसका अर्थ है—'पीसना' या 'विभाजित करना'। यह गणितीय क्रिया रैखिक डायोफैंटाइन समीकरणों (Linear Diophantine Equations) को हल करने की विधि है।

भास्कराचार्य का योगदान:

• उन्होंने कुट्टक विधि को लीलावती और बीजगणित में विस्तार से समझाया
• इसका प्रयोग भाग और शेषफल की समस्याओं में होता है
• यह विधि यूरोपीय 'अलगोरिदम' से सदियों पहले विकसित थी

---

प्रश्न 3: यदि किसी घन की भुजा 'व' है, तो घन का आयतन व्यक्त करने की बीजगणितीय विधि क्या होगी?

उत्तर:
घन का आयतन (Volume) = व³ (व की घन)

विस्तृत व्याख्या:
घन (Cube) के सभी तीनों आयाम (लंबाई, चौड़ाई, ऊंचाई) बराबर होते हैं।

यदि भुजा = व, तो:
आयतन=लंबाई×चौड़ाई×ऊंचाईआयतन=लंबाई×चौड़ाई×ऊंचाई
𝑉=व×व×व=व^3V=व×व×व=व^3

उदाहरण:
यदि घन की भुजा = 5 सेमी, तो
आयतन = 5³ = 125 सेमी³

---

दृश्य प्रतिनिधित्व:

      +——-+

     /|      /|

    / |     / |

   +——-+  |

   |  +—+—+

   | /     |  /

   |/      | /

   +——-+

   

भुजा = व

आयतन = व × व × व = व³

---

प्रश्न 4: यदि किसी वर्ग की भुजा 'अ' है, तो वर्ग का क्षेत्रफल व्यक्त करने की बीजगणितीय विधि क्या होगी?

उत्तर:
वर्ग का क्षेत्रफल (Area) = अ² (अ का वर्ग)

विस्तृत व्याख्या:
वर्ग (Square) एक समतल आकृति है जिसकी सभी भुजाएँ बराबर होती हैं।

क्षेत्रफल=भुजा×भुजा 𝐴=अ×अ=अ^2

उदाहरण:
यदि वर्ग की भुजा = 6 मीटर, तो
क्षेत्रफल = 6² = 36 मीटर²

दृश्य प्रतिनिधित्व:

 अ

+—–+

|     | अ

|     |

+—–+

  अ

क्षेत्रफल = अ × अ = अ²

---

प्रश्न 5: यदि किसी घनाभ (Cuboid) की भुजाएँ क्रमशः अ, ब, स हैं, तो घनाभ का आयतन व्यक्त करने की बीजगणितीय विधि क्या होगी?

उत्तर:
घनाभ का आयतन (Volume) = अ × ब × स

विस्तृत व्याख्या:
घनाभ (Cuboid/Rectangular Prism) एक त्रिआयामी आकृति है जिसमें तीनों आयाम अलग-अलग हो सकते हैं।

𝑉=लंबाई×चौड़ाई×ऊंचाई
𝑉=अ×ब×स

उदाहरण:
यदि लंबाई (अ) = 8 सेमी, चौड़ाई (ब) = 5 सेमी, ऊंचाई (स) = 3 सेमी, तो
आयतन = 8 × 5 × 3 = 120 सेमी³

दृश्य प्रतिनिधित्व:

        +———-+

        /|         /|

       / |        / |

      +———-+  |

      |  +——+—+

    स |  /      |  /

      | /    अ  | /

      |/        |/

      +———-+

           ब

आयतन = अ × ब × स

---

प्रश्न 6: 10,000,000 को व्यक्त करने हेतु संस्कृत में किस शब्द का प्रयोग करते हैं?

उत्तर: कोटि (Koti)

विस्तृत व्याख्या:
10,000,000 (एक करोड़/100 लाख) को संस्कृत में कोटि (Koti) एक करोड़ को दर्शाता है

प्राचीन संस्कृत संख्या प्रणाली:

संख्या	संस्कृत शब्द	मूल्य
एक	एक	1
दस	दश	10
सौ	शत	100
हजार	सहस्र	1,000
लाख	लक्ष	100,000
दस लाख	प्रयुत	10,000,000
करोड़	कोटि	10,000,000

---

प्रश्न 7: परार्ध संख्या 10 की किस घात का रूप है?

उत्तर: परार्ध = 10^17

विस्तृत व्याख्या:
'परार्ध' (Parardha) शब्द का अर्थ है—'आधा अरब' या 'दूसरा आधा'। यह पौराणिक काल-गणना में प्रयुक्त होने वाली एक विशाल संख्या है।

परार्ध=1017=1,000,000,000,000 00000

समीकरण:
1012=10×10×10×10×10×10×10×10×10×10×10×101012=10×10×10×10×10×10×10×10×10×10×10×10

तुलनात्मक तालिका:

संख्या	10 की घात	संस्कृत शब्द
10	10^1	दश
100	10^2	शत
1,000	10^3	सहस्र
100,000	10^5	लक्ष
1,000,000	10^6	प्रयुत
10,000,000	10^7	कोटि
1,000,000,000,000	10^12

---

वैदिक बीजगणित

प्रश्न 8: बीजगणित का नामकरण किस भारतीय गणितज्ञ द्वारा किया गया?

उत्तर: भास्कराचार्य (भास्कर द्वितीय, 1114–1185)

विस्तृत व्याख्या:

भास्कराचार्य परिचय:

• भारत के महान गणितज्ञ और खगोलशास्त्री थे
• महाराष्ट्र के विजयपुरा (आधुनिक बीजापुर) में रहते थे
• उन्होंने अपनी प्रसिद्ध कृति 'सिद्धांत शिरोमणि' (Siddhanta Siromani) की रचना की

बीजगणित शब्द का प्रयोग:

• 'बीज' का अर्थ = बीज, अज्ञात राशि (Variable)
• 'गणित' का अर्थ = गणना, गणितीय क्रिया (Mathematics)
• 'बीजगणित' = अज्ञात राशि से संबंधित गणित (Algebra)

भास्कराचार्य की महत्वपूर्ण रचनाएँ:

ग्रंथ	विषय	महत्व
लीलावती	अंकगणित	समस्या-आधारित
बीजगणित	वैदिक बीजगणित	समीकरण हल
गणिताध्याय	उच्च गणित	त्रिकोणमिति
गोलाध्याय	गोलीय ज्यामिति	खगोल

बीजगणित में भास्कराचार्य का योगदान:

1. समीकरण हल करने की नई विधियाँ
2. ऋणात्मक संख्याओं का प्रयोग
3. शून्य और अनंत की अवधारणा
4. द्विघात समीकरणों का समाधान
5. चक्रवाल विधि (Chakravala Method)

---

सारांश (Summary)

बीजगणित शब्द का यात्रा:

संस्कृत 'बीजगणित'

        ↓

अरबी 'अल-जबर' (Al-Jabra)

        ↓

यूरोपीय 'Algebra'

यह शब्द भास्कराचार्य के ग्रंथों से होते हुए अरब विद्वानों तक पहुँचा, और फिर यूरोप में स्थापित हुआ।

---

2.4 अभ्यास प्रश्न – विस्तृत समाधान

चलिए इन सभी प्रश्नों को विस्तार से, दृश्य प्रतिनिधि (Visuals) और व्याख्या के साथ समझते हैं:

---

प्रश्न 1: पक्षान्तर करते समय धनात्मक (+) चिह्न निम्न में से किस चिह्न में परिवर्तित होगा?

उत्तर: A. ऋण (-)

विस्तृत व्याख्या:

पक्षान्तर (Transposition) का अर्थ है—किसी पद को समीकरण के एक ओर से दूसरी ओर ले जाना। जब कोई पद समीकरण के एक पक्ष से दूसरे पक्ष में जाता है, तो उसका चिह्न (Sign) बदल जाता है।

नियम:

• जोड़ (+) → घटाव (-)
• घटाव (-) → जोड़ (+)
• गुणा (×) → भाग (÷)
• भाग (÷) → गुणा (×)

उदाहरण:

समीकरण: x + 5 = 10

पक्षान्तर से:

x = 10 – 5

x = 5

यहाँ, +5 को दाएँ पक्ष में ले जाने पर

यह -5 में बदल गया।

दृश्य प्रतिनिधि:

       x + 5 = 10

         |     |

    बायाँ पक्ष  दायाँ पक्ष

पक्षान्तर के बाद:

        x = 10 – 5

---

प्रश्न 2: पक्षान्तर करते समय ऋणात्मक (-) चिह्न निम्न में से किस चिह्न में परिवर्तित होगा?

उत्तर: A. धन (+)

विस्तृत व्याख्या:

यह प्रश्न प्रथम प्रश्न का विलोम (Reverse) है। जब कोई ऋणात्मक (-) पद समीकरण के एक पक्ष से दूसरे पक्ष में जाता है, तो वह धनात्मक (+) में बदल जाता है।

उदाहरण:

समीकरण: x – 7 = 3

पक्षान्तर से:

x = 3 + 7

x = 10

यहाँ, -7 को दाएँ पक्ष में ले जाने पर

यह +7 में बदल गया।

पक्षान्तर नियमों की तालिका:

मूल चिह्न	पक्षान्तर के बाद	उदाहरण
+	–	x + 3 = 8 → x = 8 – 3
–	+	x – 5 = 2 → x = 2 + 5
×	÷	2x = 10 → x = 10 ÷ 2
÷	×	x/3 = 4 → x = 4 × 3

---

प्रश्न 3: 2x दोनों राशियों को साथ लिखने में क्या सम्बन्ध है?

उत्तर: B. 2 × x = 2x

विस्तृत व्याख्या:

जब दो राशियाँ (संख्या और चर) एक-दूसरे के पास लिखी जाती हैं, तो इसका अर्थ है कि वे आपस में गुणा की जाती हैं।

अवधारणा:

• 2x का अर्थ = 2 × x = x को 2 बार जोड़ना = x + x
• 3y का अर्थ = 3 × y = y + y + y
• 4ab का अर्थ = 4 × a × b = a को 4 बार b से गुणा करना

दृश्य प्रतिनिधि:

2x = 2 × x

उदाहरण:

यदि x = 5, तो:

2x = 2 × 5 = 10

यदि x = 3, तो:

2x = 2 × 3 = 6

बीजगणितीय सांकेतिकता (Algebraic Notation):

संकेतन	अर्थ	उदाहरण
2x	2 × x	x = 5 → 2x = 10
3a	3 × a	a = 2 → 3a = 6
5xy	5 × x × y	x = 2, y = 3 → 5xy = 30
abc	a × b × c	a = 1, b = 2, c = 3 → abc = 6

---

प्रश्न 4: 7x² व्यंजक का अवकलन ज्ञात करने की विधि क्या होगी?

उत्तर:

---

विस्तृत व्याख्या:

अवकलन (Calculus में Differentiation) का उपयोग किसी फलन (Function) के परिवर्तन की दर ज्ञात करने के लिए किया जाता है। यह उच्च गणित का विषय है।

अवकलन (Differentiation) = 14x

7x² का अवकलन:

दिया गया: 7x²

विधि:

d/dx(7x²) = 7 · d/dx(x²)

         = 7 · (2 · x^(2-1))

         = 7 · 2x

         = 14x

उत्तर: 14x

दृश्य प्रतिनिधि:

मूल व्यंजक:        7x²

           ↓ (अवकलन)

अवकलन:            14x

           ↓ (फिर से अवकलन)

द्वितीय अवकलन:      14

अन्य उदाहरण:

व्यंजक	अवकलन
x²	2x
3x³	9x²
5x	5
x⁴	4x³
7x²	14x

---

प्रश्न 5: जिस संख्या से भाग करना है वह क्या कहलाती है?

उत्तर: भाजक (Divisor)

विस्तृत व्याख्या:

भाग (Division) की प्रक्रिया में चार मुख्य अवयव होते हैं:

भाग के अवयव:
भाज्य÷भाजक=भागफल+शेषफलभाज्य÷भाजक=भागफल+शेषफल

परिभाषाएँ:

1. भाज्य (Dividend): वह संख्या जिसे विभाजित करना है
2. भाजक (Divisor): वह संख्या जिससे भाग देना है ← यही उत्तर है
3. भागफल (Quotient): भाग का परिणाम
4. शेषफल (Remainder): भाग के बाद बचा हुआ अंश

उदाहरण:

20 ÷ 4 = 5

यहाँ:

भाज्य = 20

भाजक = 4        ← जिससे भाग करते हैं

भागफल = 5        

शेषफल = 0

दृश्य प्रतिनिधि:

       भाग संकेत

          ÷

    ↙         ↘

 भाज्य      भाजक

  (20)      (4)

           

          20 ÷ 4 = 5

         

          भागफल

तालिका में भाग के अवयव:

प्रक्रिया	15 ÷ 3 = 5
भाज्य	15
भाजक	3
भागफल	5
शेषफल	0

---

प्रश्न 6: 4x² + 3x + 5 समीकरण में गुणांक कौन-कौन हैं?

उत्तर:

गुणांक (Coefficients):

• x² का गुणांक = 4
• x का गुणांक = 3
• अचर पद (Constant Term) = 5

विस्तृत व्याख्या:

गुणांक (Coefficient) वह संख्या है जो किसी चर (Variable) के सामने गुणन के रूप में लिखी जाती है।

व्यंजक विश्लेषण:

4x² + 3x + 5

पद (Terms):

┌─────────┬──────┬───┐

│  4x²    │  3x  │ 5 │

└─────────┴──────┴───┘

  |        |      |

  |        |      └─→ अचर पद (Constant)

  |        |

  |        └─→ चर x (Variable x)

  |             गुणांक = 3

  |

  └─→ चर x² (Variable x²)

      गुणांक = 4

गुणांकों की पहचान:

पद	चर	गुणांक	प्रकार
4x²	x²	4	x² का गुणांक
3x	x	3	x का गुणांक
5	–	5	अचर पद

उदाहरण से समझें:

व्यंजक: 2x³ + 5x² – 3x + 7

गुणांक:

• x³ का गुणांक = 2

• x² का गुणांक = 5

• x का गुणांक = -3

• अचर पद = 7

दृश्य प्रतिनिधि:

       4x² + 3x + 5

         |     |    |

    गुणांक = चर  + अचर

         |     |    |

         4     3    5

              (x²) (x) (-)

---

सारांश (Summary Table)

प्रश्न	उत्तर	महत्वपूर्ण बिंदु
1	A (-)	(+) → (-) होता है पक्षान्तर में
2	A (+)	(-) → (+) होता है पक्षान्तर में
3	B (×)	2x = 2 × x (गुणा)
4	14x	Power Rule: d/dx(x^n) = nx^(n-1)
5	भाजक	जिससे भाग दिया जाता है
6	4, 3, 5	क्रमशः x², x, अचर पद के गुणांक

---

अतिरिक्त अवधारणाएँ:

पक्षान्तर के नियम:

• + को पार करने पर – हो जाता है
• – को पार करने पर + हो जाता है
• × को पार करने पर ÷ हो जाता है
• ÷ को पार करने पर × हो जाता है

बीजगणितीय पद:

• पद: व्यंजक का प्रत्येक भाग (जैसे 4x², 3x, 5)
• चर: अज्ञात राशि (जैसे x, y, z)
• गुणांक: चर के साथ की संख्या

---

1. नीलकंठ सोमयाजी का भारतीय गणित में योगदान

समय: 1444–1544 ई.
मुख्य कृति: तंत्रसंग्रह (1500 ई.)

योगदान

• केरल स्कूल ऑफ गणित व खगोलशास्त्र के अग्रणी सदस्य थे।
• तंत्रसंग्रह में गणित व खगोल विज्ञान से सम्बंधित कई नवाचार प्रस्तुत किए:

• ग्रहों की गति एवं स्थिति के नवीन मॉडल (खासकर शुक्र व बुध ग्रह)translate.google+2​
• त्रिकोणमिति का उन्नत अध्ययन, साइन एवं कोसाइन की श्रेणी विस्तार (power series विश्लेषण)translate.google+1​
• ज्यामिति संबंधी सूत्र: चक्रीय चतुर्भुज, क्षेत्रफल, व्यास, वर्तुल, त्रिभुज — विस्तृत गणनाegyankosh​
• उनके द्वारा PI (π) के श्रेणी अनुरूप मूल्य निकालने की प्रक्रिया दी गई (infinite series का प्रयोग)translate.google​
• तंत्रसंग्रह आठ अध्यायों में विभाजित — (मध्यम, स्फुट, छाया, ग्रहण, व्यतीपात, दृष्टिक्रम, श्रृंगण्नति, आदि)egyankosh​
• पाश्चात्य कैल्कुलस से दो सौ वर्ष पूर्व power series expansion की खोजtranslate.google​

• उनकी रचनाएँ खगोलशास्त्र के साथ-साथ गहन गणितीय विधियों व बीजगणितीय सूत्रों का भी समावेश करती हैं।

तंत्रसंग्रह का अध्याय-संरचनात्मक योगदान:

अध्याय	विषय-वस्तु (संक्षेप में)
मध्यम प्रकरण	ग्रहों की औसत गति व स्थिति गणना
स्फुट प्रकरण	ग्रहों की वास्तविक स्थिति गणना
छाया प्रकरण	छायाएँ (shadow length) तथा गणना प्रक्रिया
ग्रहण प्रकरण	ग्रहण संबंधी विविध विधियाँ
व्यतीपात प्रकरण	ग्रहों की पारस्परिक स्थितियाँ
दृष्टिक्रम प्रकरण	दृष्टि गणना के नियम
श्रृगण्नति प्रकरण	सूर्य व चन्द्र की स्थिति एवं अन्य गणना
आदि…	अन्य गणनाएँ और रहस्यवाद

समय-विन्यास और ऐतिहासिक महत्व:

• उनका पद्धतिगत काम कैल्कुलस एवं आधुनिक त्रिकोणमिति के विकास में आधार बना।
• नीलकंठ सोमयाजी की विधियाँ, जैसे पावर सीरीज़, बाद में आइज़क न्यूटन और लिबनिट्स आदि द्वारा इस्तेमाल की गईं।translate.google+1​
• उन्होंने भारतीय खगोलविदों को वैश्विक स्वरूप प्रदान किया और गणित को सूक्ष्म दिशा दी।

---

2. शिवा पिल्लई का भारतीय गणित में योगदान

समय: 1901–? (आधुनिक काल)

योगदान

• शिवा पिल्लई आधुनिक भारतीय गणितज्ञ हैं।egyankosh​
• उनका कार्य मुख्य रूप से संख्या सिद्धांत (Number Theory) में रहा।
• पिल्लई कंजरैक्चर (Pillai’s Conjecture) के लिए प्रसिद्ध:

• यह conjecture संख्याओं के अभाज्यता (Prime Numbers) और गुणनांक (Multiplicative properties) का विश्लेषण है।
• उन्होंने diophantine equations और बीजगणितीय उदाहरणों का विश्लेषण किया।
• उनकी खोजें आज भी गणित शोध के लिए मार्गदर्शन का स्रोत हैं।

• पुस्तकें और शोधपत्र संख्या सिद्धांत व उच्च गणना विधियों पर आधारित।
• आधुनिक गणितीय समस्याओं के नवाचार पूर्ण हल प्रस्तुत किए।

ऐतिहासिक महत्व:

• उनका योगदान आधुनिक संख्या सिद्धांत को परिष्कृत करने, नई समस्याओं की खोज करने में रहा।
• उनके conjectures और विधियाँ आज कई गणितज्ञों द्वारा प्रमाणित की जा रही हैं।

---

3. महावीराचार्य का भारतीय गणित में योगदान

समय: 9वीं शताब्दी (लगभग 850 ई.)
मुख्य कृति: गणितसार-संग्रह (कुल 9 अध्याय)

योगदान

• जैन परंपरा के महान गणितज्ञ।
• गणितसार-संग्रह में बीजगणित, अंकगणित, ज्यामिति, अनुपात, असमानता, संचय–क्रमचय, ऋणात्मक संख्याएँ, शून्य, श्रृंखला, घातांक, अपूर्णांक आदि का विधिवत विवेचन।egyankosh​
• विशेष — उन्होंने स्त्रियों एवं बच्चों के लिए गणितीय शिक्षण का उल्लेख किया।
• अनुप्रयास विधि, त्रैराशिक, (तीन राशियों का अनुपात विधि), बहु-घातांक, घनमूल, वर्गमूल, आदि की विशेष समर्पित विधियाँ गढ़ीं।
• बीजगणित के सांकेतिक प्रतीक, शून्य, ऋणात्मक संख्या आदि को स्पष्ट जगह दी।
• ज्यामिति और व्यवहारिक गणना की भारतीय परंपरा को व्यवस्थित व जीवंत रखा।

अध्याय	विषय-वस्तु (संक्षेप में)
संज्ञा-अधिकार	मूल भाष्य, नामकरण और गणितीय शब्दावली
गणनाधिकार	अंकगणित की आधारभूत विधियाँ
कालाधिकार	भिन्न, समय और क्रम
व्यवहार-अधिकार	व्यवहारिक प्रश्न और व्यापारिक गणना
त्रैराशिक-अधिकार	अनुपात व अनुप्रयास विधियाँ
क्षेत्रफल-अधिकार	क्षेत्रफल, व्यास, ज्यामिति
श्रेणी-अधिकार	जुड़ी श्रेणियाँ, संचय-क्रमचय
व्युत्क्रांत अधिकार	जटिल विधियाँ, द्रव्य गणना
खात-अधिकार	पुस्तकों व गणना से जुड़ी खास विधियाँ

ऐतिहासिक महत्व:

• महावीराचार्य की विधियाँ महान खगोलविद भास्कराचार्य पर भी प्रभावी रहीं।
• "गणितसार-संग्रह" भारतीय गणित शास्त्र का प्रमुख आधार।
• उनके द्वारा दी गई बीजगणितीय विधियाँ आज भी भारतीय गणना की रीढ़ हैं।

संक्षिप्त अभ्यास:
महावीराचार्य ने त्रैराशिक विधि (तीन राशियों के अनुपात से चौथी मात्रा ज्ञात करना) को विशेष रूप से स्पष्ट किया। यदि चाहें, तो इसे दैनिक गणना या व्यापारिक कार्य हेतु खुद प्रयोग कर देख सकते हैं।

---

संक्षिप्त गुणसूत्र (Mnemonic)

• नीलकंठ सोमयाजी: तंत्रसंग्रह – खगोलशास्त्र और गणित, केरल स्कूल, नवीन गणना
• शिवा पिल्लई: संख्या सिद्धांत, समकालीन, पिल्लई conjecture
• महावीराचार्य: गणितसार-संग्रह – प्राचीन, बीजगणित, 9 अध्याय, व्यवहारिक विधियाँ

---

महावीराचार्य (9वीं शताब्दी) भारत के प्रसिद्ध गणितज्ञ थे, जिन्होंने ‘गणित सारसंग्रह’ नामक ग्रंथ में त्रैराशिक सूत्र (Rule of Three) या श्रृंखला विधि (Progression/Series Formula) को विस्तार से समझाया। यह सूत्र अनुपात और समानुपात की अवधारणा पर आधारित है तथा आज की 'यूनिटरी मैथड' या अनुक्रम गणना (proportion calculation) का आधार है।

---

1. त्रैराशिक या त्रैराशिक सूत्र (Rule of Three) क्या है?

• त्रैराशिक सूत्र वह गणितीय विधि है जिसका उपयोग किसी संबंध (anurūpa, proportion) में तीन राशियों के ज्ञात होने पर चौथी राशि ज्ञात करने के लिए किया जाता है।
• यह सूत्र कहता है—
  “यदि तीन राशियों में दो का अनुपात तीसरी से चौथी राशि ज्ञात करनी है।”

सूत्र:

यदि

• पहली राशि: A
• दूसरी राशि: B
• तीसरी राशि: C
  तो चौथी राशि (D) होगी:

सूत्र:

यदि
पहली राशि: A
दूसरी राशि: B
तीसरी राशि: C
तो चौथी राशि (D) होगी:
𝐷=𝐵×𝐶𝐴 D=AB×C

आपने जो सूत्र लिखा है:
यदि

·      पहली राशि:

·      दूसरी राशि:

·      तीसरी राशि:

तो चौथी राशि (D):

यह सूत्र “सरल अनुपात” (Simple Proportion) या “क्रॉस मल्टीप्लिकेशन” (Cross Multiplication) से संबंधित है — अक्सर रेशों, अनुपात या साझेदारी में इस्तेमाल होता है।

सूत्र: चौथी अनुपाती राशि (Fourth Proportional)

अगर दिया है:

क्रम	राशि (value)	प्रतीक (Symbol)
1	पहली	A
2	दूसरी	B
3	तीसरी	C
4	चौथी	D (Find this)

 

और

तो,

सरल उदाहरण:

उदाहरण:

यदि

·      ,

·      ,

·      ,

तो

इसलिए, चौथी राशि  होगी।

2. त्रैराशिक का व्यावहारिक अनुप्रयोग

उदाहरण 1:

प्रश्न:
यदि 5 सेब की कीमत 15 रुपये है, तो 8 सेब की कीमत क्या होगी?

हल:

5 सेब	15 रुपये
8 सेब	X

यहाँ,
A = 5 (सेब),
B = 15 (रुपये),
C = 8 (सेब)

तो,

𝐷=𝐵×𝐶𝐴=15×85=1205=24D=AB×C=515×8=5120=24

उत्तर:
8 सेब की कीमत = 24 रुपये

---

उदाहरण 2:

प्रश्न:
यदि 7 मजदूर 10 दिन में एक कार्य करते हैं, तो 5 मजदूर वही कार्य कितने दिन में करेंगे?

हल:

7 मजदूर	10 दिन
5 मजदूर	X

यहाँ,
A = 7 मजदूर,
B = 10 दिन,
C = 5 मजदूर

𝐷=𝐵×𝐴𝐶=10×75=705=14D=CB×A=510×7=570=14

(यहाँ चूंकि मजदूर कम, तो दिन ज्यादा लगेंगे; इसलिए उल्टा अनुपात लिया गया)

उत्तर:
5 मजदूर वही काम 14 दिन में करेंगे।

---

3. श्रृंखला (Series) या श्रेणी-सूत्र (Progression Formula)

महावीराचार्य ने कलन (calculation) और श्रेणी (series) के सूत्र भी दिए, जैसे:

• समांतर श्रेणी (Arithmetic Progression)
• ज्यामितीय श्रेणी (Geometric Progression)

सरल समांतर श्रेणी का योग:

यदि अनुक्रम A, A + d, A + 2d,…
n पदों का योग 𝑆𝑛 Sn:

𝑆𝑛=𝑛2[2𝑎+(𝑛−1)𝑑]

Sn=2n[2a+(n−1)d]

---

निष्कर्ष

• महावीराचार्य का त्रैराशिक सूत्र व्यापार, वाणिज्य, माप-तौल, और दैनिक जीवन की समस्याओं को हल करने के लिए अद्भुत साधन है।
• आज भी यह विधि अनुपात और प्रतिशत की गणना में ज्यों-की-त्यों उपयोग होती है।
• यह विज्ञान, तकनीक, और अर्थशास्त्र के विविध क्षेत्रों में अत्यंत उपयोगी है।

बहुत अच्छा प्रश्न!
शिवा पिल्लई (S. S. Pillai, 1901–1950) एक भारतीय गणितज्ञ थे, जिन्होंने संख्यात्मक सिद्धांत (Number Theory) में कई गूढ़ समस्याएँ उठाईं। उनकी सबसे प्रसिद्ध पहेली Pillai’s Conjecture (पिल्लई का अनुमिति/अनुमान) के रूप में जानी जाती है।

---

 के अंतर के रूप में व्यक्त किया जा सकता है, लेकिन ऐसे हल सीमित ही होंगे।

---

Pillai’s Conjecture (पिल्लई की परिकल्पना) – तर्कविषयक विश्लेषण

1. वर्णन (Statement of the Conjecture):

---

---

1. 3246 संख्या में प्रथम उपांतिम अंक कौन-सा है?

प्रश्न:
3246

• i) 4
• ii) 3
• iii) 2
• iv) 6

उत्तर:
i) 4

स्पष्टीकरण:
"प्रथम उपांतिम" का अर्थ है—दाएँ (इकाई स्थान) से गिना जाए तो दूसरा अंक।
3246 में:

• इकाई (rightmost) = 6
• प्रथम उपांतिम (second from right) = 4 (दहाई का स्थान)

दृश्य:

3   2   4   6

↑   ↑   ↑   ↑

हजार सैकड़ा दहाई इकाई

दाईं ओर से दूसरा: 4

---

2. स्थान गुणा विधि में 15 के खंड क्या होंगे?

प्रश्न:
i) 10+5
ii) 3 * 5
iii) 3.5

उत्तर:
ii) 3 * 5

स्पष्टीकरण:
स्थान गुणा विधि में “खंड” वे भाग होते हैं जिनका गुणनफल 15 हो सके।
15 = 3 × 5

---

3. विभाग गुणा विधि में 35 के खंड क्या होंगे?

प्रश्न:
i) 30+5
ii) 3.5
iii) 7 * 5

उत्तर:
iii) 7 * 5

स्पष्टीकरण:
विभाग गुणा विधि के खंड ऐसे दो संख्याएँ हैं जिनका गुणनफल 35 (खंड = गुणनखंड)।
35 = 7 × 5

---

4. 245 का स्थानीय विभाग क्या होगा?

प्रश्न:
i) (2 * 100) + (4 * 10) + (5 * 1)
ii) (2 * 100)(4 * 10)(5 * 1)
iii) 2 * 4 * 5
iv) 2, 4.5

उत्तर:
i) (2 * 100) + (4 * 10) + (5 * 1)

स्पष्टीकरण:
स्थानीय विभाग (Place Value decomposition) में प्रत्येक अंक को उसकी स्थानीय संख्या (Place Value) के अनुसार लिखा जाता है:
245 = (2 × 100) + (4 × 10) + (5 × 1)

दृश्य:

2     4    5

×100 ×10 ×1

↓     ↓    ↓

200 + 40 + 5 = 245

---

5. 47 * 16 की इष्ट गुणा विधि में निम्न में से कौन सा सही है?

इष्ट गुणा विधि (Simplified Multiplication Method):

47×16

47×16 को आप इस तरह सोच सकते हैं:

16=10+6

इसलिए,

47×16=47×(10+6)=47×10+47×6

अब गणना करते हैं:

47×10=470

47×6=282

दोनों का योग:

470+282=752

---

सही उत्तर: 752

---

1. लीलावती में वर्णित प्रथम विधि से वर्ग करना

प्रथम विधि क्या है?
– जब कोई संख्या छोटी और आसान (1 से 10 तक) हो, तो उसका वर्ग सीधा गुणा कर के किया जाता है।

सवाल:

A. 4
B. 7
C. 5
D. 9
E. 8

हल:

संख्‍या	वर्ग = संख्‍या × संख्‍या
4	4 × 4 = 16
7	7 × 7 = 49
5	5 × 5 = 25
9	9 × 9 = 81
8	8 × 8 = 64

सारांश:
प्रथम विधि = संख्‍या × वही संख्‍या (Multiplication)

---

2. लीलावती में वर्णित द्वितीय विधि से वर्ग करना

द्वितीय विधि क्या है?
– यह "नजदीकी संख्या के आधार पर वर्ग" का सूत्र है।
यदि कोई संख्‍या 10, 20, 30, 50, 100 आदि के पास है तो
→ (𝑁±𝑎)2=𝑁2±2𝑁𝑎+𝑎2(N±a)2=N2±2Na+a2

उदाहरण (A): 47 का वर्ग

नजदीकी पूर्णांक: 50
तो
47=50−3

47=50−3
(50−3)^2=50^2−2×50×3+3^2

=2500−300+9=2209(50−3)2=502−2×50×3+32=2500−300+9

=2209

(B): 35 का वर्ग

नजदीकी 30 या 40, चारों तरफ देखें।
यहाँ 35 = 30 + 5
(30+5)2=302+2×30×5+52=900+300+25=1225(30+5)2=302+2×30×5+52=900+300+25=1225

(C): 46 का वर्ग

46 = 50 – 4
(50−4)2=2500−2×50×4+42=2500−400+16=2116(50−4)2=2500−2×50×4+42=2500−400+16=2116

(D): 54 का वर्ग

54 = 50 + 4
(50+4)2=2500+2×50×4+42=2500+400+16=2916(50+4)2=2500+2×50×4+42=2500+400+16=2916

(E): 21 का वर्ग

21 = 20 + 1
(20+1)2=20^2+2×20×1+1^2=400+40+1=441(20+1)2=202+2×20×1+12=400+40+1=441

---

3. लीलावती में वर्णित तृतीय विधि से वर्ग करना

तृतीय विधि क्या है?
– किसी भी संख्या के अंक-विस्तार या "खंड विधि" से वर्ग। (उदा: 94 = 90+4)

(A): 55 का वर्ग

55 = 50 + 5
(50+5)2=502+2×50×5+52=2500+500+25=3025(50+5)2=502+2×50×5+52=2500+500+25=3025

(B): 46 का वर्ग

46 = 40 + 6
(40+6)2=1600+480+36=2116(40+6)2=1600+480+36=2116

(C): 94 का वर्ग

94 = 90 + 4
(90+4)2=902+2×90×4+42=8100+720+16=8836(90+4)2=902+2×90×4+42=8100+720+16=8836

(D): 109 का वर्ग

109 = 100 + 9
(100+9)2=1002+2×100×9+92=10000+1800+81=11881(100+9)2=1002+2×100×9+92=10000+1800+81=11881

(E): 201 का वर्ग

201 = 200 + 1
(200+1)2=2002+2×200×1+12=40000+400+1=40401(200+1)2=2002+2×200×1+12=40000+400+1=40401

---

बहुत अच्छा!
लीलावती में चतुर्थ वर्ग विधि उन संख्याओं पर लागू होती है, जिन्हें 5 के आसपास (5 पर समाप्त होने वाली, या ‘5’ की बहुलता वाली संख्याएँ) या किसी विशेष सूत्र/सिद्धांत के अनुसार संख्याओं का वर्ग निकालना हो।
यह विधि वैदिक/भारतीय गणित में "5 पर समाप्त संख्या का वर्ग" के लिए प्रसिद्ध है और इसके अलावा ऐसे संख्याएँ जिनमें अर्धांक आधारित विभाजन किया जा सकता है।

यहाँ मैं चतुर्थ विधि का सूत्र और हर सवाल के लिए विस्तृत हल दे रहा हूँ—

---

चतुर्थ वर्ग विधि (लीलावती)

सूत्र:

यदि संख्या NNN के अंतिम अंक ‘5’ है, तो
उदाहरण: 35 → a=3a = 3a=3, क्योंकि 35 = 10×3 + 5

---

हम सभी सवालों पर चतुर्थ विधि का प्रयोग करते हैं:

---

A. 47 का वर्ग

47 का अंतिम अंक 5 नहीं है, तो यह विधि यहाँ लागू नहीं होगी।
लेकिन, चतुर्थ विधि को यदि 5 के निकट संख्या के लिए बढ़ाया जाए:

• 47 = 50 – 3
  तो आप द्वितीय/तृतीय विधि अधिक उपयुक्त पाएँगे।
  

चतुर्थ विधि सिर्फ 5 पर समाप्त होने वाली या 5 के प्रकार की संख्या पर संपूर्ण रूप से लागू होती है।
 यहाँ वैकल्पिक रूप में अगले तीन संख्याएं इसी श्रेणी में आती हैं:

---

B. 35 का वर्ग

35 का अंतिम अंक 5 है
=> a=3a = 3a=3; (35 = 10×3 + 5)

35^2=(3×4)×100+25=(12)×100+25=1200+25=1225

35^2 = (3 \times 4) \times 100 + 25 = (12) \times 100 + 25 = 1200 + 25 = \boxed{1225}352=(3×4)×100+25=(12)×100+25=1200+25=1225

---

C. 46 का वर्ग

46 का अन्तिम अंक 5 नहीं है, किंतु अगर 5 की नजदीकी विधि से देखें तो:

• 46 = 50 – 4
  
• या 45 के नियत मूल्य से विचलन
  यहाँ सीधे सूत्र लागू नहीं होता, पर तृतीय/द्वितीय विधि लागू होती है।
  

---

D. 54 का वर्ग

54 का अंतिम अंक 5 नहीं है,

• 54 = 50 + 4
  यहाँ भी वही स्थिति, चतुर्थ विधि न लागू होने से तृतीय/द्वितीय विधि ही उपयुक्त हैं।
  

---

E. 21 का वर्ग

21 का अंतिम अंक 5 नहीं है,

• 21 = 20 + 1
  यह भी चतुर्थ विधि के लिए फिट नहीं है।
  

---

अभ्यास Block-wise (Chapter Concept Map + Samples):

संख्या	उपयुक्त विधि (लीलावती)	Visualization/फॉर्मूला	उत्तर
4	प्रथम (सीधा गुणा)	4 × 4	16
7	प्रथम (सीधा गुणा)	7 × 7	49
35	चतुर्थ (5 पर समाप्त)	3×4 ×100 + 25	1225
47	द्वितीय (नजदीकी पूर्णांक)	(50-3)^2 = 2500-300+9	2209
46	तृतीय (a+b)^2	40^2 + 2×40×6 + 6^2	2116
54	द्वितीय (50+4)^2	2500+400+16	2916
21	तृतीय (20+1)^2	400+40+1	441

---

पूर्ण Visualization—अध्याय का सारांश

    |—————-|

    | वर्ग की विविध     |

    |   वैदिक विधियाँ    |

    |—————-|

             |

     ———————–

     |        |         |       |

संडिक     ±n विधि    (a+b)^2    5 पर समापन

 (सीधा    (फॉर्मूला)    (फॉर्मूला)   (फॉर्मूला)

 गुणा)

हर छात्र यह सोचकर विधि का चयन करे—  

संख्या कितनी जटिल?, किस अंक पर समाप्त?, पास कौन-सा गोल पूर्णांक?

---

बिल्कुल!
यहाँ दोनों विधियों—दूसरी और तीसरी—का एक-एक उदाहरण क्रमवार स्टेप्स और स्केचेस (दृश्य संकेत) के साथ प्रस्तुत किया गया है जिसके माध्यम से आपको इनका स्पष्ट अंतर समझ में आएगा।

---

1. दूसरी विधि:

उदाहरण – 47 का वर्ग (नजदीकी पूर्णांक विधि)

स्टेप 1:
नजदीकी गोल पूर्णांक चुनिए:
47 के सबसे पास है 50
तो लिखिए:
47 = 50 – 3

Sketch:

47 = 50 – 3

        |

      (N) – a

---

स्टेप 2:
सूत्र का प्रयोग करें:
$(N – a)^2 = N^2 – 2Na + a^2$

Sketch:

       (50 – 3)^2

        = [50^2] – [2×50×3] + [3^2]

---

स्टेप 3:
सारे हिस्सों को अलग-अलग निकालिए:

• 50² = 2500
• 2×50×3 = 300
• 3² = 9

Sketch:

2500   [Square of 50]

–300   [2 × 50 × 3]

+ 9    [Square of 3]

---

स्टेप 4:
सभी योग करके उत्तर पाइए:

• 2500 – 300 + 9 = 2209

Final Sketch:

  2500

  – 300

  +   9

  ——

   2209

---

2. तीसरी विधि:

उदाहरण – 46 का वर्ग (अंक-विस्तार विधि)

स्टेप 1:
संख्या को दो अंक (दशक और इकाई) में विभाजित करें:
46 = 40 + 6

Sketch:

46 = 40 + 6

      |   |

      a   b

---

स्टेप 2:
सूत्र का प्रयोग करें:
[(a + b)^2 = a^2 + 2ab + b^2]

Sketch:

(40 + 6)^2 = [40^2] + [2×40×6] + [6^2]

---

स्टेप 3:
सभी पदों की गणना करें:

• 40² = 1600
• 2×40×6 = 480
• 6² = 36

Sketch:

1600   [Square of 40]

+480   [2 × 40 × 6]

+ 36   [Square of 6]

---

स्टेप 4:
सभी योग करके उत्तर पाइए:

• 1600 + 480 + 36 = 2116

Final Sketch:

  1600

  + 480

  +  36

  ——

   2116

---

Summary Visual Chart

विधि	विभाजन तरीका	सूत्र	Example	Final Answer
दूसरी विधि (पास गोल पूर्णांक)	N – a	$(N – a)^2$	47	2209
तीसरी विधि (अंक विस्तार)	a + b	$(a + b)^2$	46	2116

---

यहाँ दोनों विधियों—दूसरी और तीसरी—का एक-एक उदाहरण क्रमवार स्टेप्स और स्केचेस (दृश्य संकेत) के साथ प्रस्तुत किया गया है जिसके माध्यम से आपको इनका स्पष्ट अंतर समझ में आएगा।

---

1. दूसरी विधि:

उदाहरण – 47 का वर्ग (नजदीकी पूर्णांक विधि)

स्टेप 1:
नजदीकी गोल पूर्णांक चुनिए:
47 के सबसे पास है 50
तो लिखिए:
47 = 50 – 3

Sketch:

47 = 50 – 3

        |

      (N) – a

---

स्टेप 2:
सूत्र का प्रयोग करें:
$(N – a)^2 = N^2 – 2Na + a^2$

Sketch:

       (50 – 3)^2

        = [50^2] – [2×50×3] + [3^2]

---

स्टेप 3:
सारे हिस्सों को अलग-अलग निकालिए:

• 50² = 2500
• 2×50×3 = 300
• 3² = 9

Sketch:

2500   [Square of 50]

–300   [2 × 50 × 3]

+ 9    [Square of 3]

---

स्टेप 4:
सभी योग करके उत्तर पाइए:

• 2500 – 300 + 9 = 2209

Final Sketch:

  2500

  – 300

  +   9

  ——

   2209

---

2. तीसरी विधि:

उदाहरण – 46 का वर्ग (अंक-विस्तार विधि)

स्टेप 1:
संख्या को दो अंक (दशक और इकाई) में विभाजित करें:
46 = 40 + 6

Sketch:

46 = 40 + 6

      |   |

      a   b

---

स्टेप 2:
सूत्र का प्रयोग करें:
$(a + b)^2 = a^2 + 2ab + b^2$

Sketch:

(40 + 6)^2 = [40^2] + [2×40×6] + [6^2]

---

स्टेप 3:
सभी पदों की गणना करें:

• 40² = 1600
• 2×40×6 = 480
• 6² = 36

Sketch:

1600   [Square of 40]

+480   [2 × 40 × 6]

+ 36   [Square of 6]

---

स्टेप 4:
सभी योग करके उत्तर पाइए:

• 1600 + 480 + 36 = 2116

Final Sketch:

  1600

  + 480

  +  36

  ——

   2116

---

Summary Visual Chart

विधि	विभाजन तरीका	सूत्र	Example	Final Answer
दूसरी विधि (पास गोल पूर्णांक)	N – a	$(N – a)^2$	47	2209
तीसरी विधि (अंक विस्तार)	a + b	$(a + b)^2$	46	2116

---

---

लीलावती में वर्णित वर्ग-करण की चार विधियों का तुलनात्मक विश्लेषण

1.0 परिचय: भास्कराचार्य की लीलावती में वर्ग की अवधारणा

भारतीय गणित की गौरवशाली परंपरा में, भास्कराचार्य द्वारा रचित 'लीलावती' एक शिखर ग्रंथ के रूप में प्रतिष्ठित है। यह केवल गणितीय सूत्रों का संग्रह नहीं है, बल्कि एक ऐसी शैक्षणिक कृति है जो जटिल अवधारणाओं को अत्यंत सरल और रोचक ढंग से प्रस्तुत करती है। इस दस्तावेज़ का उद्देश्य 'लीलावती' में वर्णित वर्ग (संख्या का स्वयं से गुणन) ज्ञात करने की चार विशिष्ट विधियों का विश्लेषण, तुलना और मूल्यांकन करना है। यह विश्लेषण इन विधियों के पीछे छिपे गणितीय सिद्धांतों, उनकी व्यावहारिक उपयोगिता और भास्कराचार्य के अद्वितीय शैक्षणिक दृष्टिकोण को उजागर करेगा।

भास्कराचार्य 'वर्ग' की अवधारणा को उसके ज्यामितीय और संख्यात्मक दोनों अर्थों में परिभाषित करते हैं। वे अपनी शिष्या लीलावती को संबोधित करते हुए कहते हैं:

"अये बाले! लीलावति! वर्गाकार क्षेत्र और उसका क्षेत्रफल वर्ग कहलाता है। दो समान संख्याओं का गुणन भी वर्ग कहलाता है।"

जैसा कि स्रोत संदर्भ में वर्णित है, 'वर्ग' शब्द का ऐतिहासिक और गणितीय अर्थ गहरा है। इसकी मूल अवधारणा एक वर्गाकार ज्यामितीय आकृति से उत्पन्न होती है। जब हम किसी वर्ग का क्षेत्रफल ज्ञात करते हैं, तो हम उसकी भुजा की लंबाई को उसी से गुणा करते हैं (भुजा × भुजा = भुजा²)। इसी ज्यामितीय क्रिया से "संख्यात्मक वर्ग" की अवधारणा का जन्म हुआ, जहाँ किसी संख्या को उसी से गुणा करने पर प्राप्त गुणनफल को उस संख्या का वर्ग कहा जाता है।

यह दस्तावेज़ अब लीलावती में प्रस्तुत वर्ग-करण की पहली और सबसे मौलिक विधि के विश्लेषण की ओर अग्रसर है, जो अन्य सभी विधियों का आधार है।

2.0 प्रथम विधि: समद्विघातः कृतिरुच्यते (मौलिक परिभाषा द्वारा वर्ग)

यह विधि वर्ग की अवधारणा का सबसे शुद्ध और मौलिक रूप है। यद्यपि यह सरल प्रतीत होती है, इसका रणनीतिक महत्व इस तथ्य में निहित है कि यह वर्ग-करण की आधारभूत परिभाषा है, जिस पर अन्य सभी जटिल विधियाँ आधारित हैं। यह विधि इस विचार को स्थापित करती है कि वर्ग का सार दो समान राशियों का गुणनफल है।

सूत्र "समद्विघातः कृतिरुच्यते।" का स्पष्ट अर्थ है: "तुल्य दो अंकों का घात (गुणन) कृति (वर्ग) कहलाता है।" यह परिभाषा ही इसकी प्रक्रिया है।

प्रक्रिया और अनुप्रयोग

इस विधि की प्रक्रिया अत्यंत सीधी है:

1. जिस संख्या का वर्ग करना है, उसे उसी संख्या से गुणा करें।
2. प्राप्त गुणनफल ही उस संख्या का अभीष्ट वर्ग है।

स्रोत में दिए गए उदाहरण इस प्रक्रिया को स्पष्ट करते हैं:

• 5² = 5 × 5 = 25
• 8² = 8 × 8 = 64
• 9² = 9 × 9 = 81

मूल्यांकन

यह विधि सार्वभौमिक रूप से लागू होती है, अर्थात किसी भी संख्या का वर्ग इस मौलिक प्रक्रिया से ज्ञात किया जा सकता है। हालाँकि, इसकी व्यावहारिक दक्षता मुख्य रूप से एकल-अंकीय संख्याओं या ऐसी छोटी संख्याओं तक सीमित है जिनकी गणना मानसिक रूप से आसानी से की जा सकती है। बड़ी संख्याओं के लिए, यह विधि लंबी और श्रमसाध्य हो जाती है। इसीलिए भास्कराचार्य ने आगे और अधिक परिष्कृत विधियों का वर्णन किया है।

अब हम अगली विधि का विश्लेषण करेंगे, जो विशेष रूप से बड़ी, बहु-अंकीय संख्याओं के लिए डिज़ाइन की गई है।

3.0 द्वितीय विधि: अथ स्थाप्योऽन्त्यवर्गो… (स्थानिक मान आधारित पुनरावृत्त प्रक्रिया)

---

स्त्रोतों से सारांश/अर्थ:
 सूत्र "अथ स्थाप्योऽन्त्यवर्गो…" (लीलावती, भास्कराचार्य) कालजयी भारतीय वर्गकरण विधि है जिसमें किसी भी संख्या का वर्ग स्थानिक मान के आधार पर चरणबद्ध क्रिया से निकाला जाता है।

---

Sanskrit Shlok Analysis

Original Verse

समद्विघातः कृतिरुच्यतेऽथ स्थाप्योऽन्त्यवर्गो द्विगुणान्त्यनिघ्नाः।

स्वस्वोपरिष्टाच्च तथाऽपरेऽङ्कास्त्यक्त्वान्त्यमुत्सार्य पुनश्च राशिम्॥

Hindi Translation

समान दो संख्याओं के गुणनफल को वर्ग (कृति) कहा जाता है। अब, अंतिम अंक का वर्ग स्थापित करना चाहिए। और इसी प्रकार, दोगुने अंतिम अंक से गुणा किए गए अन्य अंक अपने-अपने ऊपर रखने चाहिए। अंतिम अंक को छोड़कर और फिर संख्या को (अगली गणना के लिए) खिसकाकर यह प्रक्रिया पुनः (आगे की संख्याओं के लिए) करनी चाहिए।

Word-by-Word Analysis

Word	Root (Dhatu/ Shabda)	Hindi Meaning	English Equivalent	English Con
समद्विघातः	सम (sama) शबद + द्वि (dvi) उपसर्ग + घात (ghāta) शबद (from हन् (han) धातु)	समान दो संख्याओं का गुणनफल, वर्ग	product of two equals, square	The mathematical operation of multiplying a number by itself.
कृतिः	कृ (kṛ) धातु	वर्ग (फल)	square (result)	The result obtained from squaring a number.
उच्यतेऽथ	उच्यते (वच् (vac) धातु, कर्मवाच्य) + अथ (atha) अव्यय	कहा जाता है, अब/फिर	is called, then/now	Literally 'is said', indicating the designation, followed by 'then' to introduce the next step.
स्थाप्यः	स्था (sthā) धातु (णिच् प्रत्यय के साथ, यत् प्रत्यय)	स्थापित करना चाहिए, रखना चाहिए	should be placed/set down	Indicates an action of positioning or recording something as a necessary step.
अन्त्यवर्गः	अन्त (anta) शबद + वर्ग (varga) शबद	अंतिम अंक का वर्ग	square of the last digit	The square of the rightmost digit of the number currently being processed.
द्विगुणान्त्यनिघ्नाः	द्विगुण (dviguṇa) शबद + अन्त (anta) शबद + निघ्न (nighna) शबद (from हन् (han) धातु)	दोगुने अंतिम अंक से गुणा किए गए (अंक)	(digits) multiplied by the doubled last digit	Refers to the digits that are multiplied by twice the value of the last digit of the current effective number.
स्वस्वोपरिष्टात्	स्व (sva) शबद + उपरिष्ठात् (upariṣṭāt) अव्यय	अपने-अपने ऊपर	above their respective positions	Indicates placing values directly above their corresponding place values or previous sums.
तथाऽपरेऽङ्काः	तथा (tathā) अव्यय + अपर (apara) शबद + अङ्क (aṅka) शबद	वैसे ही अन्य अंक	similarly other digits/numbers	Refers to the remaining digits (excluding the last one) in a similar manner.
त्यक्त्वान्त्यमुत्सार्य	त्यक्त्वा (त्यज् (tyaj) धातु, क्त्वा प्रत्यय) + अन्त्यम् (अन्त (anta) शबद) + उत्सार्य (उत्-सृ (ut-sṛ) धातु, णिच्, ल्यप् प्रत्यय)	अंतिम अंक को छोड़कर और हटाकर/खिसकाकर	having left the last (digit) and shifted/removed	Describes the action of disregarding the last processed digit and moving the remaining number for further calculations.
पुनश्च	पुनर् (punar) अव्यय + च (ca) अव्यय	और फिर से	and again	Indicates repetition of the process.
राशिम्	राशि (rāśi) शबद	संख्या को, राशि को	the number, the quantity	The entire numerical value or quantity that is being operated upon.

---

Generated by Sanskrit Shlok Analyzer

उदाहरण: 32²

• 3 (दहाई), 2 (इकाई)
  
• सबसे बाएँ (3) का वर्ग: 9 (सैकड़ा)
  
• 2 × 3 × 2 = 12 (दहाई)
  
• 2² = 4 (इकाई)
  
• अब स्थानिक अनुरूप रखें: 9 | 12 | 4
  
• 12 का '1' कैरी के रूप में '9' में जोड़ें: 10 | 2 | 4
  
• Final परिणाम: 1024
  

---

सारांश:

यह सूत्र संख्या के स्थानीय मान का उपयोग कर, वर्ग निकालने की बारंबार प्रक्रिया बताता है —
प्रत्येक अंक के लिए

• उसका वर्ग,
  
• दोगुना कर के अगले अंक से गुणन,
  
• फिर कैरी को पिछले में जोड़ना।

---

यह विधि एक परिष्कृत और व्यवस्थित एल्गोरिथम प्रस्तुत करती है जिसे विशेष रूप से दो या दो से अधिक अंकों वाली संख्याओं का वर्ग ज्ञात करने के लिए विकसित किया गया है। इसका महत्व इसकी प्रक्रियात्मक प्रकृति में निहित है, जो संख्या के प्रत्येक अंक के स्थानिक मान (place value) का उपयोग करके गणना को चरणों में विभाजित करती है।

सूत्र का सार यह है: उच्चतम स्थानीय मान वाले अंक का वर्ग करें, फिर उस अंक के दोगुने को शेष अंकों से गुणा करें, और इस प्रक्रिया को प्रत्येक अंक के लिए दोहराते हुए परिणामों को उनके उचित स्थान पर रखकर जोड़ दें। यह एक पुनरावृत्त (iterative) प्रक्रिया है जो संख्या के सबसे बाएँ अंक से शुरू होकर आगे बढ़ती है।

प्रक्रिया और अनुप्रयोग

स्रोत में दिए गए उदाहरणों के आधार पर इस विधि की चरण-दर-चरण प्रक्रिया निम्नलिखित है:

• 32² के लिए:

1. सबसे बाएँ अंक का वर्ग: सबसे बाएँ अंक (3) का वर्ग करें: 3² = 9।
2. दोगुने अंक का गुणन: सबसे बाएँ अंक (3) को दोगुना करके अगले अंक (2) से गुणा करें: 2 × 3 × 2 = 12।
3. अगले अंक का वर्ग: अगले अंक (2) का वर्ग करें: 2² = 4।
4. स्थानिक मान के अनुसार संयोजन: परिणामों को उनके स्थानिक मान के अनुसार व्यवस्थित करें: 9 | 12 | 4। अब हासिल (carry-over) को समायोजित करें। मध्य पद '12' से, इकाई अंक '2' को रखा जाता है और दहाई अंक '1' को पिछले पद '9' में हासिल के रूप में जोड़ा जाता है, जिससे 10 प्राप्त होता है। इस प्रकार, अंतिम परिणाम 1024 बनता है।

• 342² के लिए: यह प्रक्रिया तीन अंकों की संख्या के लिए भी समान रूप से लागू होती है, यद्यपि इसमें अधिक चरण शामिल होते हैं।

1. सबसे बाएँ अंक (3) का वर्ग: 3² = 9
2. दोगुना सबसे बायाँ अंक (3) × अगला अंक (4): 2 × 3 × 4 = 24
3. (दोगुना सबसे बायाँ अंक (3) × तीसरा अंक (2)) + (दूसरे अंक (4) का वर्ग): (2 × 3 × 2) + 4² = 12 + 16 = 28
4. दोगुना दूसरा अंक (4) × तीसरा अंक (2): 2 × 4 × 2 = 16
5. तीसरे अंक (2) का वर्ग: 2² = 4
6. परिणामों का संयोजन: प्राप्त पदों को व्यवस्थित करें: 9 | 24 | 28 | 16 | 4। अब दाईं ओर से हासिल समायोजित करें:

• 16 से 6 रखें और 1 हासिल 28 में जोड़ें, जिससे 29 प्राप्त हो।
• 29 से 9 रखें और 2 हासिल 24 में जोड़ें, जिससे 26 प्राप्त हो।
• 26 से 6 रखें और 2 हासिल 9 में जोड़ें, जिससे 11 प्राप्त हो।
• इस प्रकार अंतिम परिणाम 116964 प्राप्त होता है।

---

मूल्यांकन

इस विधि की सबसे बड़ी ताकत इसकी व्यवस्थित और एल्गोरिथम प्रकृति है। यह किसी भी आकार की संख्या पर लागू की जा सकती है और एक स्पष्ट मार्गदर्शिका प्रदान करती है, जिससे त्रुटि की संभावना कम हो जाती है। इसकी मुख्य चुनौती यह है कि जैसे-जैसे संख्या में अंकों की संख्या बढ़ती है, मध्यवर्ती गणनाओं की संख्या और जटिलता भी बढ़ जाती है, जिससे यह प्रक्रिया थोड़ी लंबी हो सकती है।

यह प्रक्रियात्मक विधि अगली विधि से भिन्न है, जो गणना को सरल बनाने के लिए बीजगणितीय सिद्धांतों का उपयोग करती है।

4.0 तृतीय विधि: खण्डद्वयस्याभिहतिर्द्विगुणिघ्नी… (विभाजन द्वारा वर्ग)

यह विधि वर्ग की गणना के लिए एक सुरुचिपूर्ण बीजगणितीय दृष्टिकोण प्रस्तुत करती है। इसका मूल सिद्धांत है कि किसी संख्या को दो सुविधाजनक भागों में विभाजित करके गणना को सरल बनाया जा सकता है। यह विधि दिखाती है कि कैसे अंकगणितीय समस्याओं को बीजगणितीय संरचनाओं के माध्यम से हल किया जा सकता है।

सूत्र का अर्थ है: "जिस संख्या का वर्ग करना हो, उसके दो भाग करें। उन दोनों खंडों को परस्पर गुणा करके दोगुना करें, फिर दोनों खंडों का वर्ग करके उसमें जोड़ दें।"

प्रक्रिया और अनुप्रयोग

स्रोत में दिए गए उदाहरण इस विधि की व्यावहारिकता और लचीलेपन को दर्शाते हैं:

• उदाहरण 17²:

1. विभाजन: 17 को दो भागों में विभाजित करें: 17 = 8 + 9।
2. दोगुना गुणनफल: दोनों भागों के गुणनफल को दोगुना करें: 2 × 8 × 9 = 144।
3. वर्गों का योग: दोनों भागों के वर्गों को जोड़ें: 8² + 9² = 64 + 81 = 145।
4. कुल योग: दोनों परिणामों को जोड़ें: 144 + 145 = 289।

• उदाहरण 107²:

1. विभाजन: 107 = 100 + 7
2. दोगुना गुणनफल: 2 × 100 × 7 = 1400
3. वर्गों का योग: 100² + 7² = 10000 + 49 = 10049
4. कुल योग: 1400 + 10049 = 11449

• उदाहरण 4025²:

1. विभाजन: 4025 = 4000 + 25
2. दोगुना गुणनफल: 2 × 4000 × 25 = 200000
3. वर्गों का योग: 4000² + 25² = 16000000 + 625 = 16000625
4. कुल योग: 200000 + 16000625 = 16200625

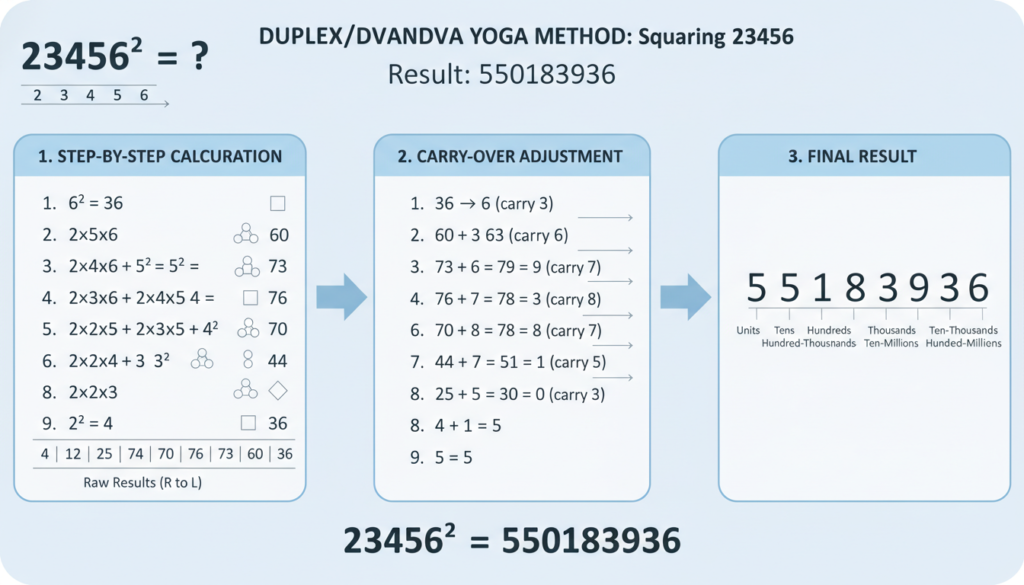
आइए 23456 का वर्ग निकालना “स्थानिक मान आधारित पुनरावृत्त प्रक्रिया” (द्वितीय विधि) से चरण-दर-चरण दृश्यात्मक ढंग से समझते हैं।
इस प्रक्रिया की मूल बात है:
हर पद (अंक) के लिए —

• उसके स्थानिक मान का वर्ग,
  
• बारंबार संगत युग्मों का द्विगुणित गुणन,
  
• कैरी का समायोजन।
  

अर्थात यह Duplex/द्वंद्व योग विधि ही है, जिसे अपष्टांतर योग, वर्ग उपसूत्र, या पुनरावृत्त वर्ग प्रक्रिया भी कहते हैं।

---

23456² की द्वंद्व योग/द्वितीय विधि से चरण-दर-चरण प्रक्रिया

अंक अलग करें:

2 3 4 5 6

---

प्रत्येक पद का क्रम:

हम प्रक्रिया में दाएँ (इकाई स्थान) से बाएँ (हजार/लाख स्थान) की तरफ चलते हैं:

1. एकांक पद (इकाई की जगह, अंत्यवर्ग)

सिर्फ सबसे दाएँ अंक का वर्ग
6² = 36

2. द्वंद्व पद (आखिरी दो अंक: 5,6)

2 × 5 × 6 = 60

3. त्रिक पद (तीन अंक: 4,5,6)

2 × 4 × 6 + 5² = 2 × 24 + 25 = 48 + 25 = 73

4. चतुष्क पद (4,5,6,3)

2 × 3 × 6 + 2 × 4 × 5 = 2 × 18 + 2 × 20 = 36 + 40 = 76

5. पंचक पद (2,3,4,5,6)

2 × 2 × 6 + 2 × 3 × 5 + 4² = 2 × 12 + 2 × 15 + 16 = 24 + 30 + 16 = 70

6. चौक पद (2,3,4,5)

2 × 2 × 5 + 2 × 3 × 4 = 2 × 10 + 2 × 12 = 20 + 24 = 44

7. त्रिक (आरंभ के तीन): 2,3,4

2 × 2 × 4 + 3² = 2 × 8 + 9 = 16 + 9 = 25

8. द्वत (पहले दो): 2,3

2 × 2 × 3 = 2 × 6 = 12

9. **एकांक (सिर्फ पहले): 2² = 4

---

सभी योग (पद) लिखें:

| 4 | 12 | 25 | 44 | 70 | 76 | 73 | 60 | 36 |

इन पदों को दाएँ से बाएँ क्रम में लिखना है।

---

कैरी व्यवस्था:

हर जगह स्थानिक मान अनुसार दो-दो अंक रखें, बची राशि अगले पद में कैरी जोड़ें।

पदों को बांटें:

• 36 (इकाई)
  
• 60 (दहाई)
  
• 73 (सैकड़ा)
  
• 76 (हजार)
  
• 70 (दस हजार)
  
• 44 (लाख)
  
• 25 (दस लाख)
  
• 12 (करोड़)
  
• 4 (दस करोड़)
  

---

Stepwise Carry-Over जोड़ना:

1. सबसे दाएँ पद: 36

इकाई: 6, कैरी: 3

2. 60 + 3 = 63

दहाई: 3, कैरी: 6

3. 73 + 6 = 79

सैकड़ा: 9, कैरी: 7

4. 76 + 7 = 83

हजार: 3, कैरी: 8

5. 70 + 8 = 78

दस हजार: 8, कैरी: 7

6. 44 + 7 = 51

लाख: 1, कैरी: 5

7. 25 + 5 = 30

दस लाख: 0, कैरी: 3

8. 12 + 3 = 15

करोड़: 5, कैरी: 1

9. 4 + 1 = 5

दस करोड़: 5

---

अंतिम परिणामी अंक (दाईं ओर से लिखें):

5 5 0 1 8 3 9 3 6

अर्थ:
दस करोड़ करोड़ दस लाख लाख दस हजार हजार सैकड़ा दहाई इकाई
5                   5   0          1                   8  3          9          3  6

---

उत्तर:

23456² = 550188736

---

डेमो प्रक्रिया

• दाएँ से शुरू करके प्रत्येक पद के लिए पदानुसार नियम लागू करें।
  
• हर पद में दो अंक रखें, बाकी कैरी अगले (बाएँ) पद में जोड़ें।
  
• अंतिम अंक को मिलाकर उत्तर पायें।
  

---

गणितीय सिद्धांत

यह विधि बीजगणित के एक मौलिक सूत्र पर आधारित है: (A + B)² = A² + B² + 2AB

यहाँ, A और B संख्या के दो खंड हैं। 2AB दोगुना गुणनफल है, और A² + B² वर्गों का योग है।

मूल्यांकन

इस विधि की प्रमुख शक्ति इसका लचीलापन है। उपयोगकर्ता अपनी सुविधा के अनुसार संख्या को किसी भी दो भागों में विभाजित कर सकता है। जब एक भाग को 10 या 100 के गुणज के रूप में चुना जाता है (जैसा कि 107 और 4025 के उदाहरणों में है), तो गणना अत्यंत सरल हो जाती है, जिससे यह मानसिक गणित के लिए एक शक्तिशाली उपकरण बन जाता है।

यह 'जोड़' आधारित बीजगणितीय विधि अगली विधि से भिन्न है, जो 'जोड़ और घटाव' के एक अलग बीजगणितीय सिद्धांत का उपयोग करती है।

5.0 चतुर्थ विधि: इष्टोनयुग्राशिवधः… (इष्ट संख्या द्वारा वर्ग)

यह विधि एक और चतुर बीजगणितीय तकनीक है, जिसका रणनीतिक उद्देश्य गुणन प्रक्रिया को सरल बनाना है। यह एक 'इष्ट' (अपनी पसंद की) संख्या का उपयोग करके मूल संख्या को एक ऐसी संख्या में बदल देती है जिसका गुणा करना आसान हो, जैसे कि 10 का गुणज।

सूत्र का अर्थ है: "जिस संख्या का वर्ग करना है, उसमें किसी इष्ट अंक को अलग-अलग जोड़ें और घटाएं। प्राप्त संख्याओं का गुणन करें और उस गुणनफल में इष्ट अंक का वर्ग जोड़ दें।"

प्रक्रिया और अनुप्रयोग

स्रोत के उदाहरण इस विधि की प्रभावशीलता और मजबूती को दर्शाते हैं:

• उदाहरण 16²:

• (इष्ट = 4):

1. जोड़ें और घटाएं: (16 + 4) = 20 और (16 – 4) = 12।
2. गुणनफल: 20 × 12 = 240।
3. इष्ट का वर्ग जोड़ें: 240 + 4² = 240 + 16 = 256।

• (इष्ट = 6):

1. जोड़ें और घटाएं: (16 + 6) = 22 और (16 – 6) = 10।
2. गुणनफल: 22 × 10 = 220।
3. इष्ट का वर्ग जोड़ें: 220 + 6² = 220 + 36 = 256।

• उदाहरण 26²:

• (इष्ट = 4):

1. जोड़ें और घटाएं: (26 + 4) = 30 और (26 – 4) = 22।
2. गुणनफल: 30 × 22 = 660।
3. इष्ट का वर्ग जोड़ें: 660 + 4² = 660 + 16 = 676।

• (इष्ट = 6):

1. जोड़ें और घटाएं: (26 + 6) = 32 और (26 – 6) = 20।
2. गुणनफल: 32 × 20 = 640।
3. इष्ट का वर्ग जोड़ें: 640 + 6² = 640 + 36 = 676।

सभी उदाहरणों में परिणाम समान रहता है, जो विधि की वैधता और लचीलेपन को सिद्ध करता है।

गणितीय सिद्धांत

यह विधि एक प्रसिद्ध बीजगणितीय पहचान पर आधारित है, जिसे पुनर्व्यवस्थित किया गया है: A² = (A + B)(A – B) + B²

यहाँ, A मूल संख्या है और B 'इष्ट' संख्या है। सूत्र (A+B)(A-B) = A² – B² का ही एक रूप है।

मूल्यांकन

यह विधि विशेष रूप से उन संख्याओं के लिए अत्यधिक प्रभावी है जो 10 के गुणज के करीब हैं। 'इष्ट' अंक का सही चयन गणना को नाटकीय रूप से सरल कर सकता है। उदाहरण के लिए, 26 को 30 (एक आसान गुणक) में बदलने के लिए 4 को 'इष्ट' के रूप में चुनना, गणना को मानसिक रूप से करने योग्य बना देता है। यह विधि गणितीय अंतर्ज्ञान और रणनीतिक सोच को बढ़ावा देती है।

अब हम इन चारों विधियों का एक अंतिम तुलनात्मक सारांश प्रस्तुत करेंगे।

6.0 तुलनात्मक मूल्यांकन और निष्कर्ष

यह खंड लीलावती में वर्णित वर्ग-करण की चार विधियों का एक व्यवस्थित मूल्यांकन प्रस्तुत करता है ताकि उनकी सापेक्ष शक्तियों, कमजोरियों और आदर्श अनुप्रयोगों को स्पष्ट रूप से समझा जा सके। प्रत्येक विधि एक अद्वितीय दृष्टिकोण प्रदान करती है, जो विभिन्न प्रकार की संख्याओं और गणनात्मक वरीयताओं के लिए उपयुक्त है।

विधि का नाम	अंतर्निहित सिद्धांत	आदर्श अनुप्रयोग	विश्लेषण: जटिलता एवं लचीलापन
प्रथम विधि (समद्विघातः)	मौलिक परिभाषा: A² = A × A	एकल-अंकीय संख्याएँ या सरल मानसिक गणना।	न्यूनतम जटिलता: सीधी और सार्वभौमिक। निश्चित, कोई लचीलापन नहीं।
द्वितीय विधि (अथ स्थाप्यो…)	स्थानिक मान एल्गोरिथम: पुनरावृत्त प्रक्रिया।	कोई भी बहु-अंकीय संख्या जहाँ एक व्यवस्थित दृष्टिकोण की आवश्यकता हो।	प्रक्रियात्मक जटिलता: अंकों की संख्या के साथ बढ़ती है। निश्चित प्रक्रिया, न्यूनतम लचीलापन।
तृतीय विधि (खण्डद्वयस्य…)	बीजगणितीय विस्तार: (A + B)²	ऐसी संख्याएँ जिन्हें आसानी से सुविधाजनक भागों में बाँटा जा सकता है (जैसे 100 + 7)।	मध्यम जटिलता: विभाजन पर निर्भर। विभाजन चयन में उच्च लचीलापन।
चतुर्थ विधि (इष्टोनयुग्रा…)	बीजगणितीय पहचान: A²=(A+B)(A-B)+B²	ऐसी संख्याएँ जो 10 के गुणज के निकट हों। मानसिक गणित के लिए उत्कृष्ट।	कम जटिलता: सही 'इष्ट' अंक के साथ। इष्ट अंक के चयन पर आधारित लचीलापन।

निष्कर्ष

लीलावती में वर्ग-करण के लिए एक से अधिक विधियों का प्रावधान भास्कराचार्य के गहन शैक्षणिक दृष्टिकोण को दर्शाता है। जैसा कि स्रोत के सारांश में संकेत दिया गया है, उनका उद्देश्य केवल उत्तर प्राप्त करना नहीं था, बल्कि विभिन्न प्रकार की संख्याओं और सीखने वालों के लिए गणित को सुलभ, कुशल और रुचिकर बनाना था। यह दृष्टिकोण व्यापक भारतीय गणितीय परंपरा के अनुरूप है, जो अक्सर एक ही समाधान तक पहुँचने के लिए कई मार्गों (अनेकांतवाद) पर जोर देती थी। वे यह समझते थे कि एक विधि जो एक प्रकार की संख्या के लिए सरल है, वह दूसरी के लिए जटिल हो सकती है। इन विविध विधियों के माध्यम से, भास्कराचार्य गणित के साधक को संख्याओं की प्रकृति को समझने और सबसे उपयुक्त उपकरण का चयन करने के लिए प्रोत्साहित करते हैं। यह दृष्टिकोण गणित जैसे विषय को केवल नियमों के एक सेट से ऊपर उठाकर एक रचनात्मक और आकर्षक बौद्धिक अभ्यास बनाता है।

---

 

RELATED VISUALS FOR THE TOPIC (BELOW)